
友人からの「そもそも機械学習ってなんなの?」「機械(コンピューター)がどうやって学習しているの?」という問いかけをきっかけに機械学習がどのようにデータを学習しているかについてコラムにしてみました。前回は決定木の回帰木という手法を紹介しました。決定木には回帰木と分類木の2種類があります。前回紹介した回帰木はお料理の得点(0点から100点)などの連続する数値を学習する時に使われます。今回紹介する分類木は「0か1か」のような2つの値を学習することができます。例えばある商品がどのような条件であれば「買われる」または「買われない」といった条件を学習することができます。それでは分類木の仕組みをみていきましょう。
INDEX
VoI1:機械学習ってなんなの?(勾配降下法)
VoI2:機械学習ってなんなの?(図解:決定木(回帰木)
決定木(分類木)
データ分析を生業にしているものとして恥ずかしいのですが、友人からのある素朴な質問にすぐに答えられなかったことがありました。それは「そもそも機械学習ってなんなの?」「機械(コンピューター)がどうやって学習してるの?」という問いかけでした。
私が考える「機械(コンピューター)がどうやって学習してるの?」への回答は「機械(コンピューター)がデータのパターンを学習(記憶)する」ために「データのパターンを自動で数式やルールにして記憶する」かなと思っています。
今は紅葉狩りの季節ではないのですが、例えば紅葉狩りに「行く」「行かない」に対して天気や気温、風の強さなどのデータがあったとします。
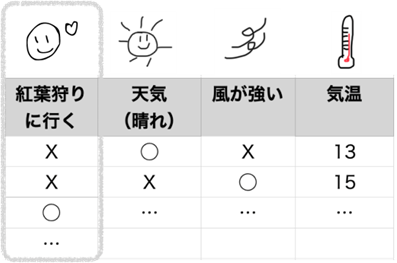
私たちであれば、データを見なくても、晴れてて、風の弱い日に紅葉狩りに行くんだろうなと想像がつきます。みなさんも、晴れていて風の弱い日にいきたいですよね?
もしデータ項目名が「단풍 사냥」「날씨」のようにハングル語で書かれていて、「단풍 사냥」の◯ / Xを、他のデータ項目のパターンで分類しなさいと言われたら私たちも「むむ」となると思います。
もちろん、コンピューターには紅葉狩りがどんなものかといった知識がありません。
それでは、コンピューターがデータから紅葉狩りに「行く」「行かない」をどのように学習していくのかを見ていきましょう。

冒頭で紹介したように今回は決定木の分類木を使用します。
決定木は、データを順番に2つに分けていって似ているグループを見つけていく仕組みです。決定木には分類木と回帰木という2種類があるのですが今回のように、紅葉狩りに行く行かないといった2つの値を学習する場合は分類木を使います。(2つ以上で分ける方法もあるのですが、2つで分ける方法を紹介します)
(回帰木は0点から100点までのような連続する値を学習することができます、回帰木については前回のコラム「機械学習ってなんなの?(決定木:回帰木)」で解説しています。もしよろしければそちらのコラムも読んでいただければ幸いです。
分類木でグループを分ける指標としてジニ不純度を使用してみましょう。
ジニ不純度はどれだけ「純粋(まじりけがない)」か、または「純粋ではない(まじりけがある)」かを表す指標です。
分類木は分類したいデータ項目(紅葉狩りに「行く」「行かない」)を別のデータ項目(天気が「晴れ」か「晴れじゃない」など)で分類したときに、分類したいデータ項目(紅葉狩りに「行く」「行かない」)がどれだけ「純粋(まじりけがない)」か、または「純粋ではない(まじりけがある)」かをジニ不純度を使って計算していきます。
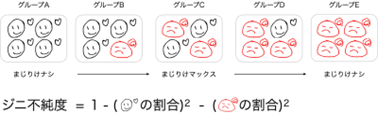
ジニ不純度は0から0.5の値をとり0に近いほど不純度が低く(まじりけがなく)理想的な分類に近い状態といえます。
それでは、ジニ不純度を使用してデータを2つに分けていく仕組みを説明していきます。
分かりやすくするために、データは7個だけ使いますね。
まずは、「天気(晴れ)」の項目を使って「天気(晴れ)= ◯」と「「天気(晴れ)= X」にグループ分けしてそれぞれのグループのジニ不純度を計算してみましょう。
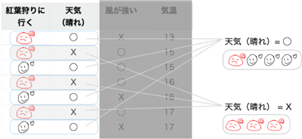


次に「天気(晴れ)」の項目でどれだけ純粋に(まじりけなく)分けられたかの指標を計算します。ジニ不純度が小さいほどまじりけがありません。 「天気(晴れ)」の項目のジニ不純度は2つに分けたグループのジニ不純度の加重平均で計算されます。下の図で確認してみましょう。
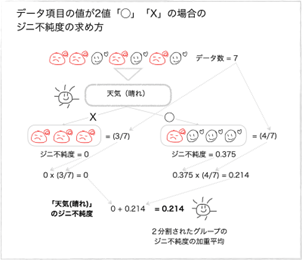
「天気(晴れ)」の項目を使ってグループを2つに分けた時のジニ不純度は0.214と計算されました。
計算式がわかったと思います。同じように「風が強い」の項目を使ってグループを2つに分けた時のジニ不純度を確認しましょう。
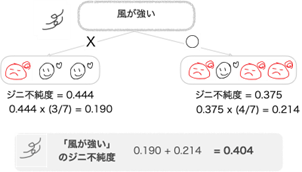
「風が強い」の項目を使ってグループを2つに分けた時のジニ不純度は0.404と計算されました。
ジニ不純度が小さいほど不純度が低いので「天気(晴れ)」=0.209と「風が強い」=0.404を比較すると「天気(晴れ)」の項目の方がジニ不純度が小さい値です。
分類木は「天気(晴れ)」の項目の方がまじりけなく分けられていると判断します。
次に気温のようにデータが「◯」「X」ではなく数値の時は、どのように分割するか見ていきましょう。
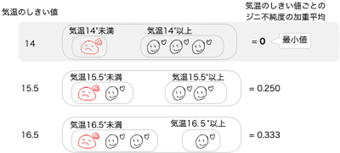
まず、データを気温が小さい順に並べます。それぞれの気温の中間をしきい値としてその値以下のグループとその値より大きいグループに分割してそれぞれのジニ不純度を計算します。
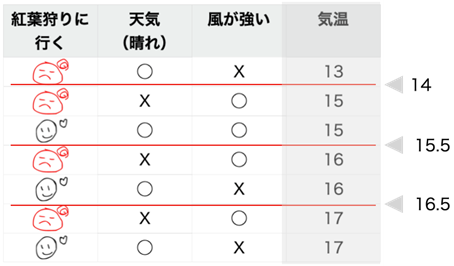
このデータの場合、気温のしきい値は「14」,「15.5」,「16.5」です。
気温のしきい値ごとにグループ分けして同じ計算式でジニ不純度の加重平均を計算します。
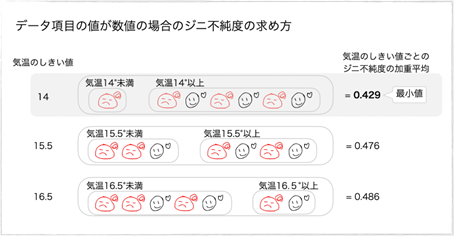
分類木は気温のジニ不純度として気温のしきい値に対してジニ不純度の加重平均の最小値の組合せを探して使用します。
ジニ不純度の最小値は気温のしきい値が「14」の時で0.429ですね。
「紅葉狩りに行く行かない」について対応する全てのデータ項目のジニ不純度が計算出来ました。
それぞれ「天気(晴れ)」=0.209、「風が強い」=0.404、「気温14°」=0.429ですね。
気温を加えても、ジニ不純度が一番小さいのは「天気(晴れ)」=0.209でした。

この結果から分類木は、「天気(晴れ)」の項目が最もまじりけなくデータを分割できると判断します。そして一番最初の分岐として「天気(晴れ)」の項目の「◯」「X」でデータを分割します。
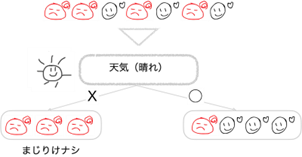
左のグループ(「天気(晴れ)」= X)は「まじりけナシ」なのでこれ以上分割出来ないですね。
分類木は次のステップとして右のグループ(「天気(晴れ)」= ◯)を「風が強い」と「気温」のデータ項目を使って分割していきます。
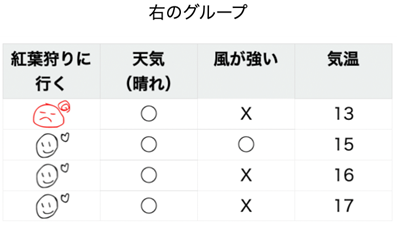
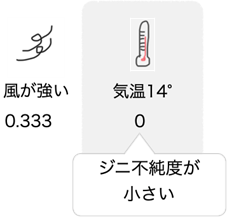
右のグループについて先ほどと同様にジニ不純度を計算していきます。 「風が強い」のジニ不純度は0.333でした。
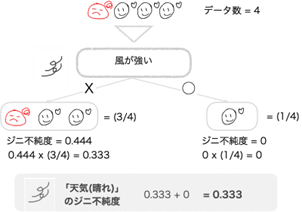
(「天気(晴れ)」= ◯)のグループの気温のしきい値も、「14」,「15.5」,「16.5」の3個ですね
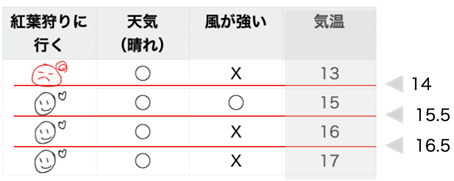
先ほどと同様、気温のしきい値ごとにグループ分けしてジニ不純度の加重平均を計算して最小値を探します。
ジニ不純度の最小値は気温のしきい値が「14」の時で0ですね。
ジニ不純度は「風が強い」=0.333、「気温14°」=0なので、決定木はジニ不純度が小さい「気温14°」を使ってデータを分類します。
この段階で全てのグループが紅葉狩りに「行く」または「行かない」にまじりけナシで分割できました。
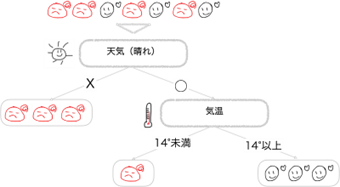
決定木の学習によってデータから紅葉に行くか行かないかを予測するルールが自動的に決められたと思います。
説明を分かりやすくするためにデータ数は7個としましたが、このデータの場合、天気が晴れで気温が14°以上の時に紅葉狩りに行く確率が高そうだという予想ができましたね。
今回の例では紅葉狩りに「行く行かない」に対応するデータ項目は(天気が晴れ、風が強い、気温)だけでしたが、対応するデータ項目(例:「性別」「年齢」…)が増えてもこの方法で対応することができます。
機械学習で予測するときには、学習したルールを学習済みモデルとして保存します。
新しいデータ(天気、風が強い、気温、性別、年齢…)が来たときに、新しいデータをこの学習済みのモデルに通すことで、そのデータについて紅葉狩りに行くか行かないかの確率を算出させているんですよ。
まとめ
冒頭の
「機械(コンピューター)がどうやって学習してるの?」への回答として
「機械(コンピューター)がデータのパターンを記憶する」ために「データのパターンを自動で数式やルールにして記憶する」ことができたと思います。
ありがとうございました。
機械学習の基礎となる知識をできるだけ簡単に説明してみました。
使い方次第では便利なツールであるというイメージを少しは持てましたでしょうか?
もし機械学習を使ったら「こんなこともできちゃうのかな?」みたいなご質問があれば
遠慮なく、お問い合わせフォームにご連絡いただければと思います。
またこのような仕事に興味がある方も積極採用しておりますので、応募お待ちしております。
関連記事



