
友人からの「そもそも機械学習ってなんなの?」「機械(コンピューター)がどうやって学習しているの?」という問いかけをきっかけに機械学習がどのようにデータを学習しているかについてコラムにしてみました。
前回は機械学習の裏側で、「実際の値」と「機械学習の計算値」の差を自動で減らしてくれる「勾配降下法」という仕組みを紹介しました。「勾配降下法」は生成AIなどが世の中にある大量の文書情報を学習する際にも使われており、縁の下の力持ちとして機械学習を支えているんですよ。 今回は、「決定木の回帰木」という手法を取り上げたいと思います。こちらはお聞きになったこともあるかもしれません、簡単に言うとデータを分岐させて学習する仕組みです。それでは回帰木がデータを学習する仕組みを見ていきましょう。
決定木(回帰木)
データ分析を生業にしているものとして恥ずかしいのですが、友人からのある素朴な質問にすぐに答えられなかったことがありました。それは「そもそも機械学習ってなんなの?」「機械(コンピューター)がどうやって学習してるの?」という問いかけでした。
私が考える「機械(コンピューター)がどうやって学習してるの?」への回答は「機械(コンピューター)がデータのパターンを学習(記憶)する」ために「データのパターンを自動で数式やルールにして記憶する」かなと思っています。
例えば、「お料理の得点(100点満点でお料理のおいしさを評価)」に対する「塩味の濃さ(塩の量)」「出汁の種類(鰹、昆布)」「出汁の量」のデータが20個あったとします。
このデータを「お料理の得点」に対する、その他のデータ(「塩味の濃さ(塩の量)」など)のパターンを機械学習で学習させてみましょう。

まずは「お料理の得点」に対する「塩味の濃さ(塩の量)」のデータ1つだけを抜き出して仕組みを理解した後に、他のデータ(出汁の種類など)も使って機械学習を完了したいと思います。
「お料理の得点」と「塩味の濃さ(塩の量)」の20個のデータをプロットしてみましょう。
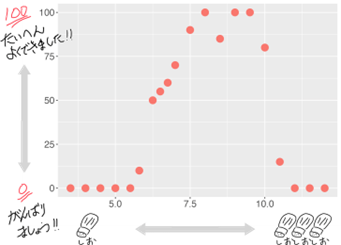
グラフにすれば「塩の量が少ないところ」と「塩の量の多いところ」に0点が多く、味が薄いんだろうとか塩辛いんだろうなど一目瞭然です。人がグラフを見れば、塩の量が6くらいより下であれば得点の低く、10を超えると得点が低いなど、塩の量で分類するのは簡単ですね。
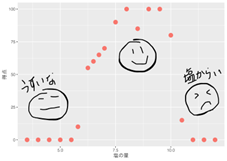
機械(コンピュータ)はこのようなデータをどのように学習するのでしょうか?
決定木という手法でどのように学習していくかを見ていきましょう。
決定木は、データを順番に2つに分けていって似ているグループを見つけていく仕組みです。決定木には分類木と回帰木という2種類があるのですが今回のように、料理の得点(0点から100点まで連続する値)を学習する場合は回帰木を使います。
(分類木は「(勝ち、負け)(◯まる、Xばつ)」などの非連続の値を学習出来ます、分類木についてはまたの機会に)
回帰木は「塩の量」の値の小さい方から順にデータのグループを2つに分けて「お料理の得点」の*バラツキの小さいところでグループ分けしていきます。
*「バラツキ」の計算にはそれぞれのデータのグループの「(平均得点と実際の得点の差)の2乗の合計」を使ってみます。
まずは「塩の量」が一番小さなデータ1個とそれ以外の19個に分けた時を計算してみましょう。
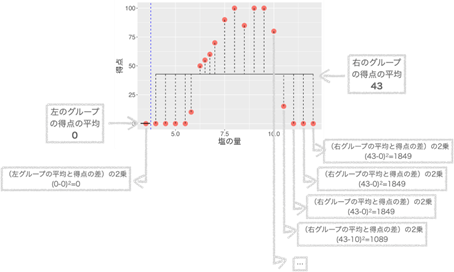
データを2つに分けた時の左と右のグループの平均得点と得点の差の2乗の合計(バラツキ)が以下に求まります。
左のグループ:(0-0)2 =0
右のグループ:(43-0)2 +(43-0)2 +(43-0)2 +(43-10)2 +…=31116
左右のグループの平均と得点の差の2乗の合計(バラツキ)=0+31116
この調子で塩の量のしきい値を順番にずらして左のグループ、右のグループの平均得点と得点の差の2乗の合計を計算します。
アニメーションにして左と右のグループの平均と得点の差の2乗の合計(バラツキ)が最も小さくなるポイントを探してみましょう。
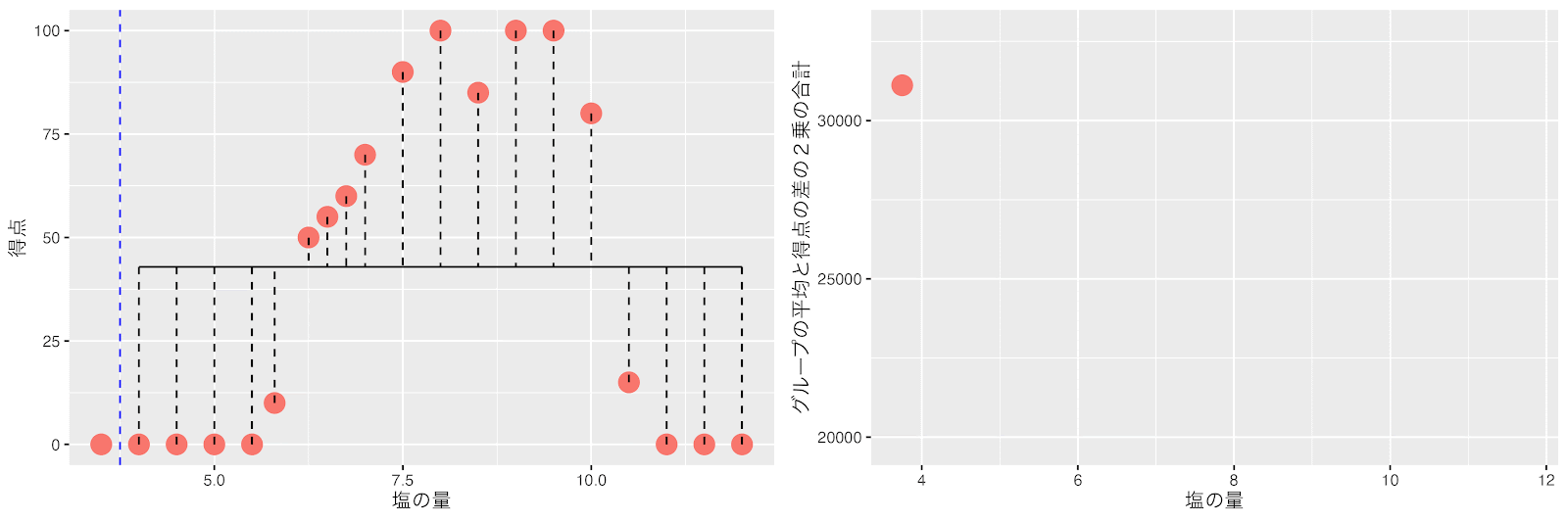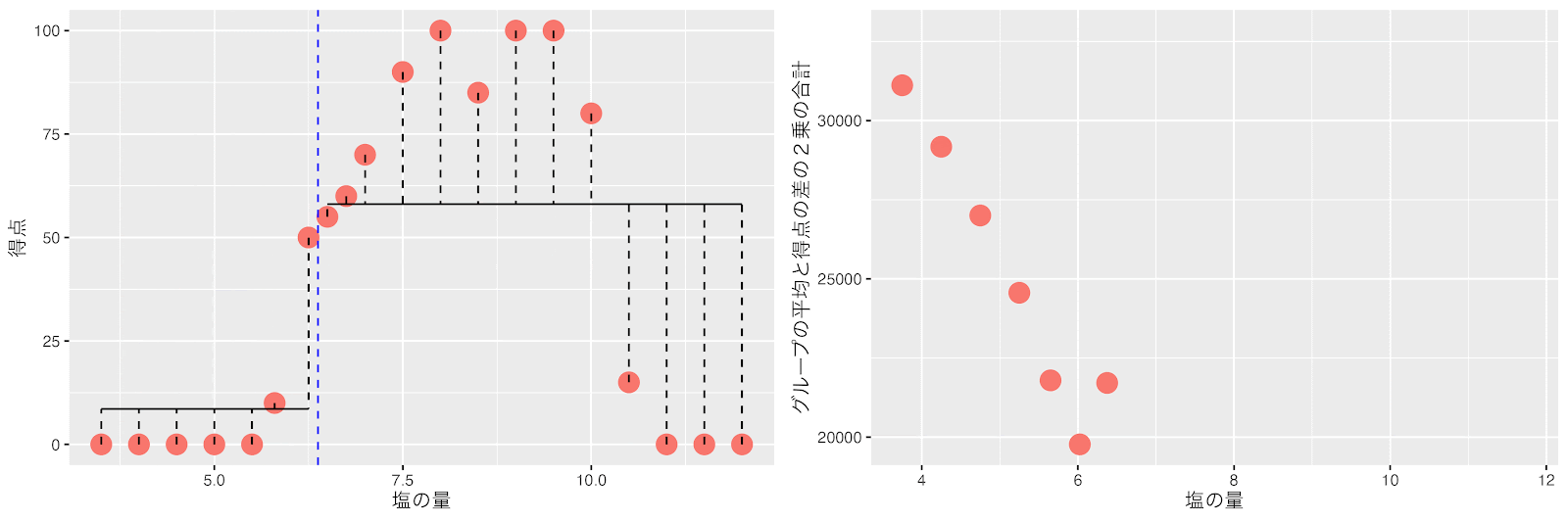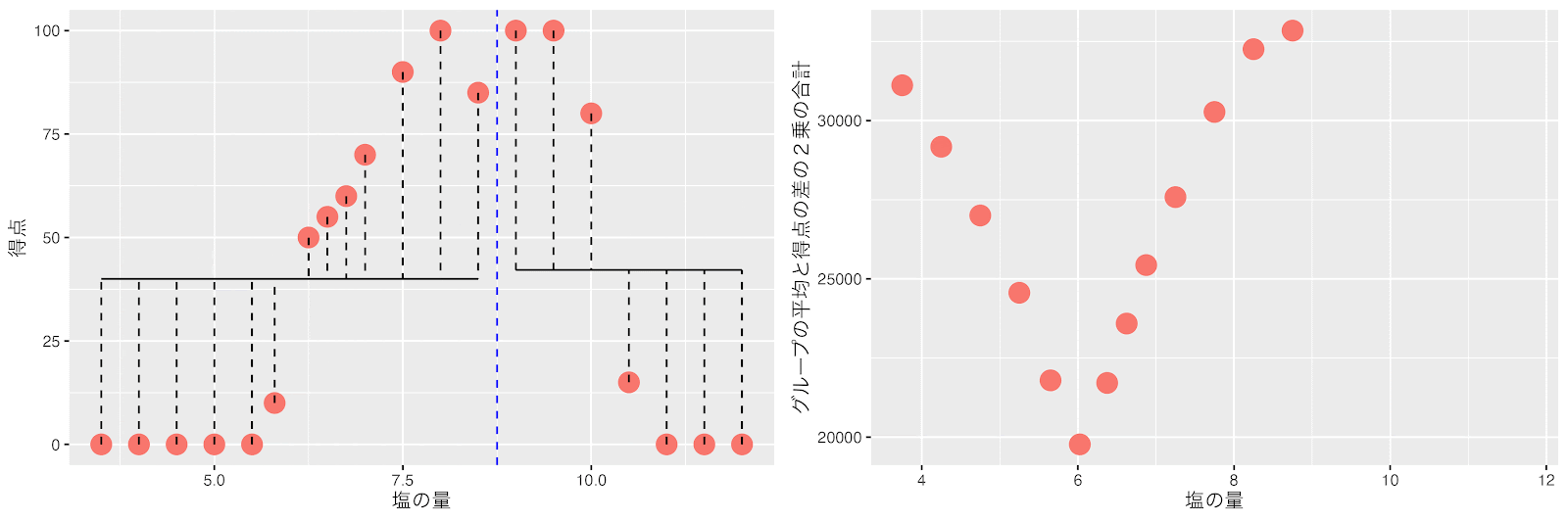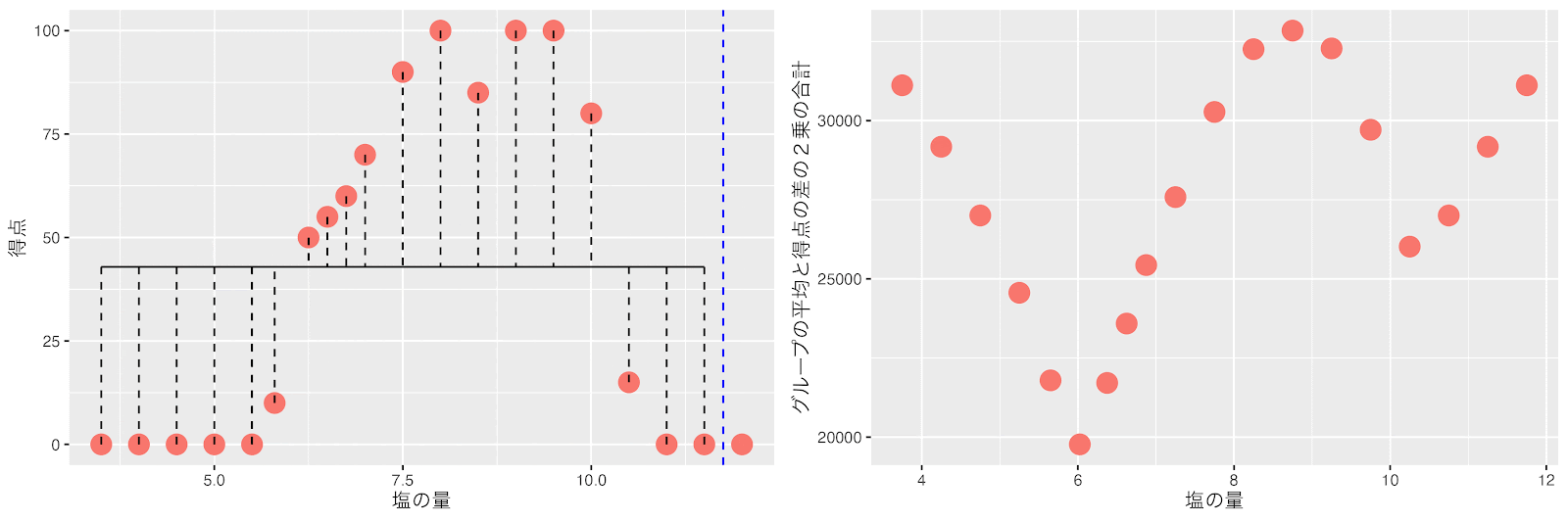
塩の量が5.8と6.2の間(6.0)が左と右のグループの平均得点と得点の差の2乗の合計(バラツキ)が最小になりました。
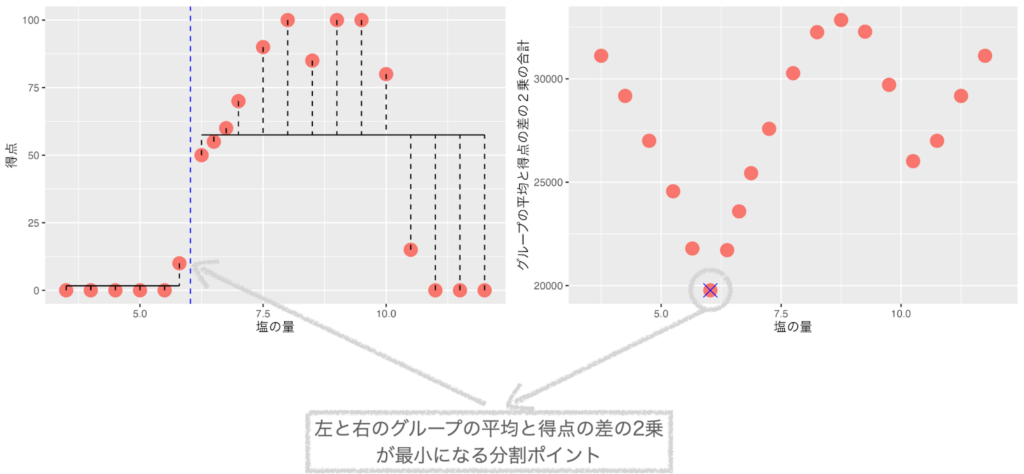
回帰木は、最初の分岐として、左と右のグループの平均得点と得点の差の2乗の合計(バラツキ)が最小になるポイント(塩の量 = 6)をしきい値にしてデータを2つのグループに分割します。
左のグループはほとんど0点ですね。
ここで、グループをそれ以上「分割する」「分割しない」というルール(グループのデータ数)を決めておきます。今回は7個としてみます。
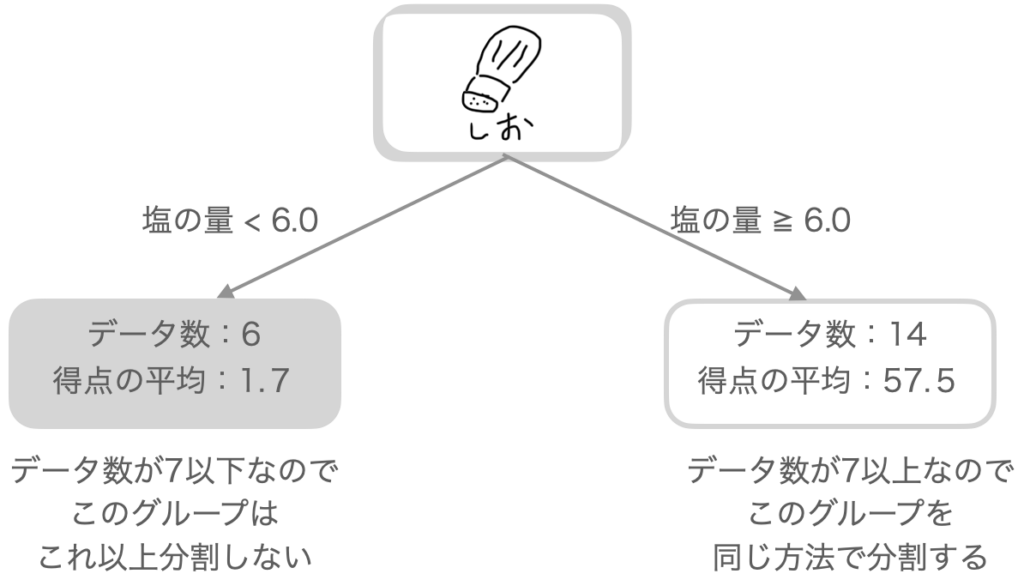
左のグループ(塩の量が6以下)はデータ数が6個で7以下なので分割しません。
一方、右のグループ(塩の量が6以上)はデータ数が14個で7以上です。
この右のグループを先ほどのように左右に分けて平均と得点の差の2乗の合計(バラツキ)が最小になるポイントを探します。
チェックポイント✔️
回帰木は「もう分割しないグループ」のデータを取り除いて、残りのデータを何度も分割していくんですよ。
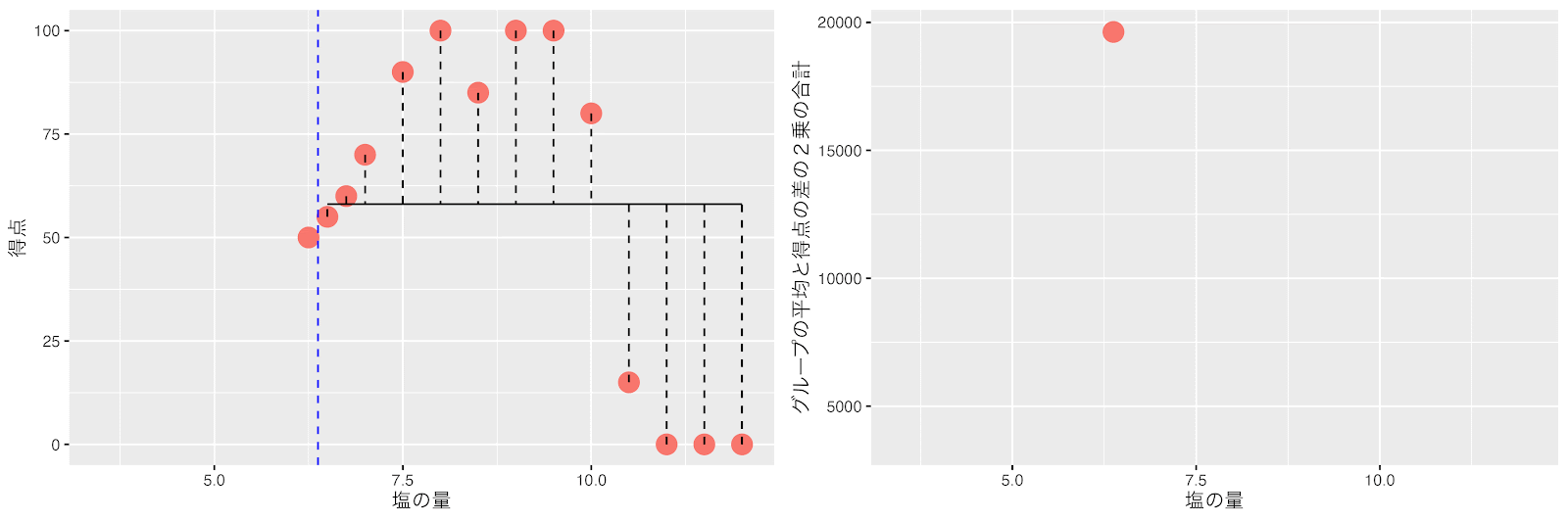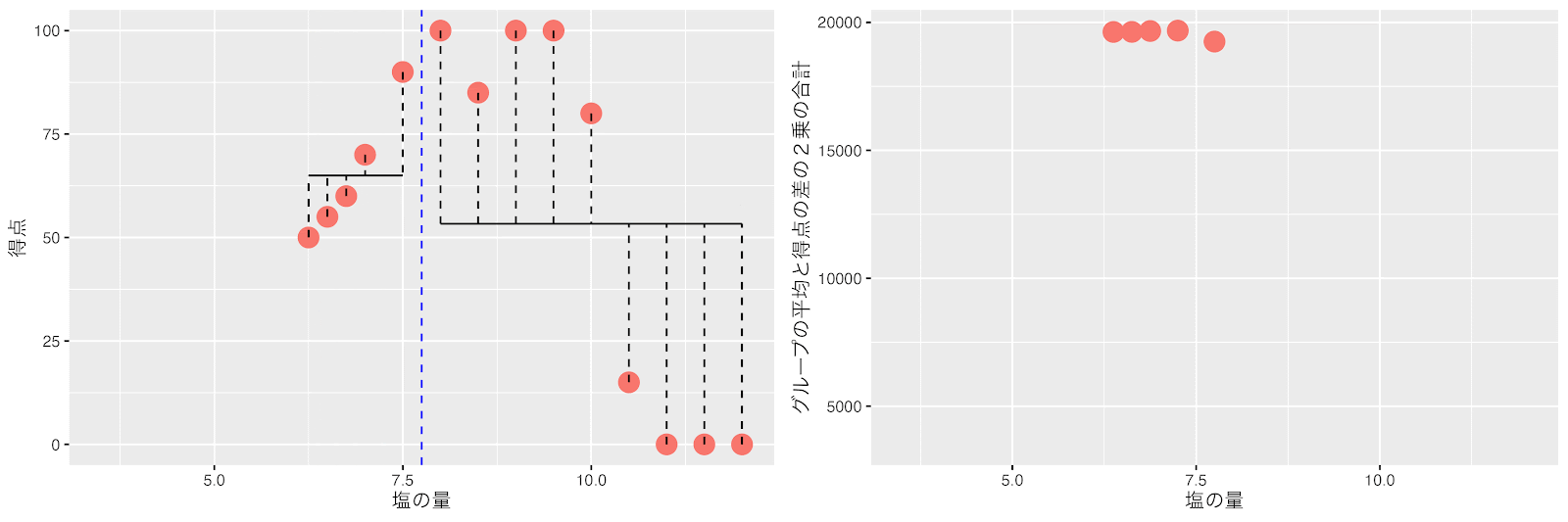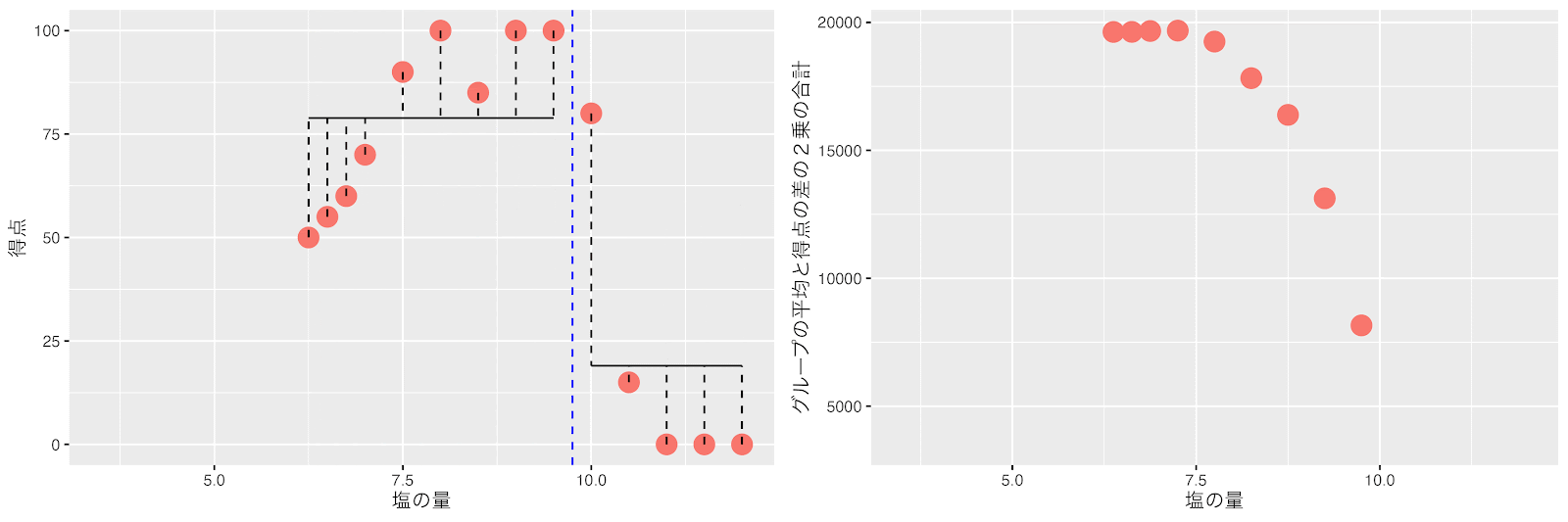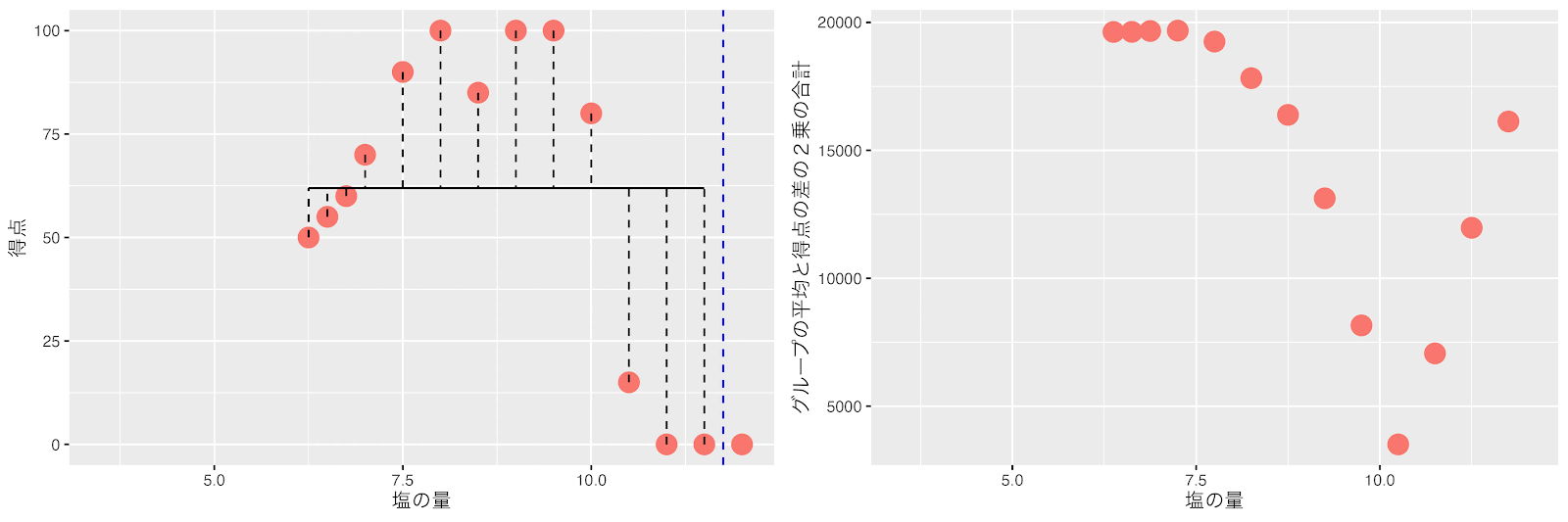
塩の量を10と10.5の間(10.25)で分けた時に左と右のグループの平均得点と得点の差の2乗の合計(バラツキ)が最小になりました。
回帰木は次の分岐として、塩の量が10.25をしきい値にしてデータを分割します。
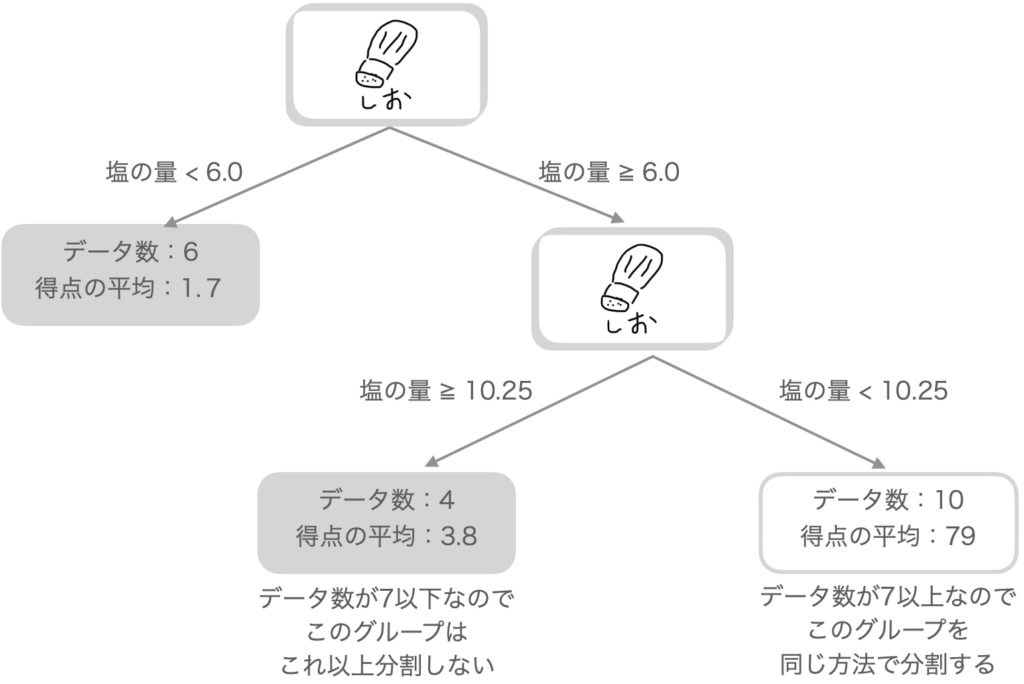
左のグループ(塩の量が10.25以上)はデータ数が4個で7以下なので分割しません。
右のグループ(塩の量が6〜10.25の範囲)はデータ数は10個で7以上です。同様に左右のグループの平均得点と得点の差の2乗の合計(バラツキ)が最小になるポイントで分割します。
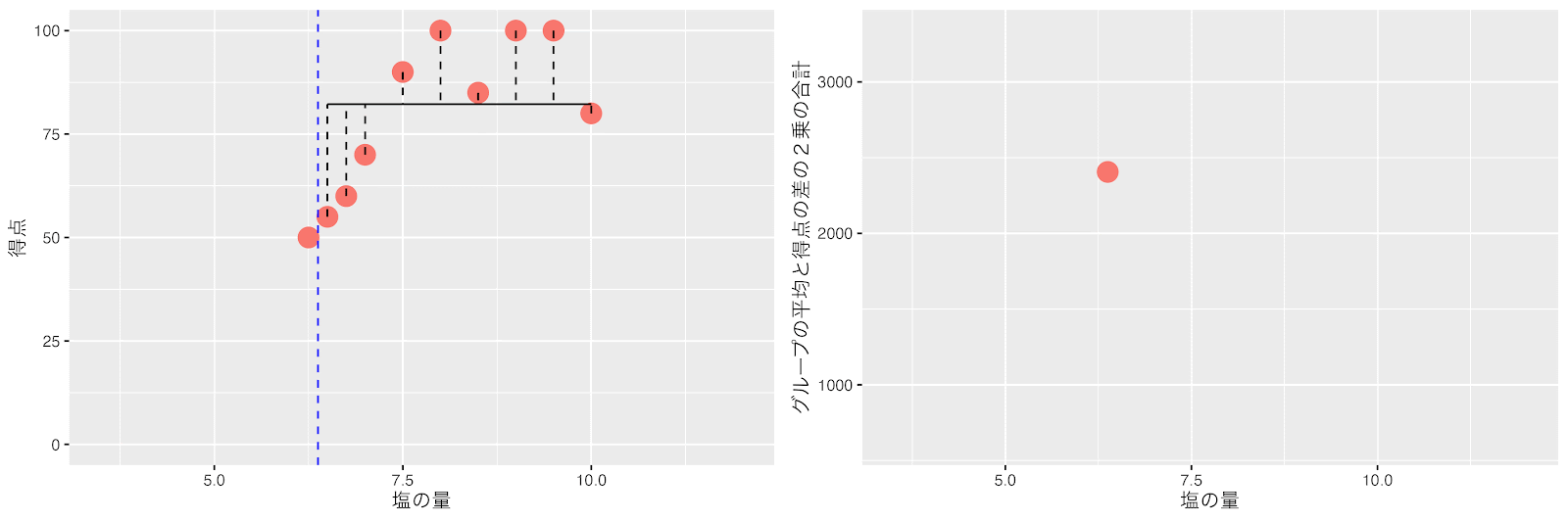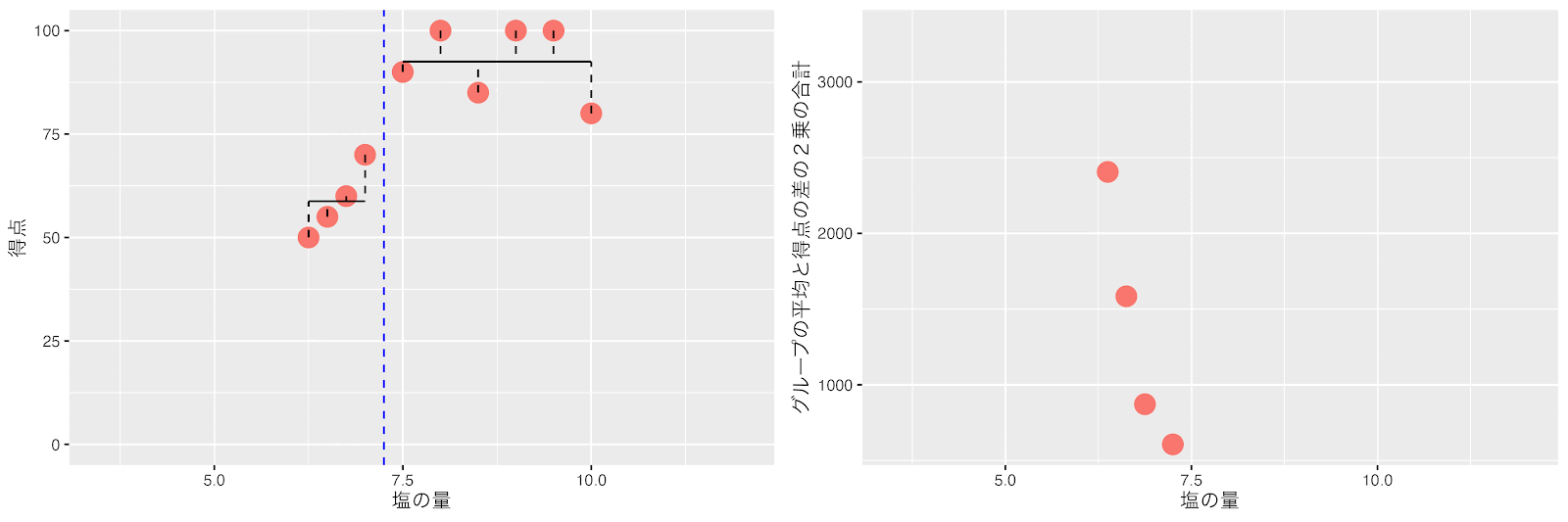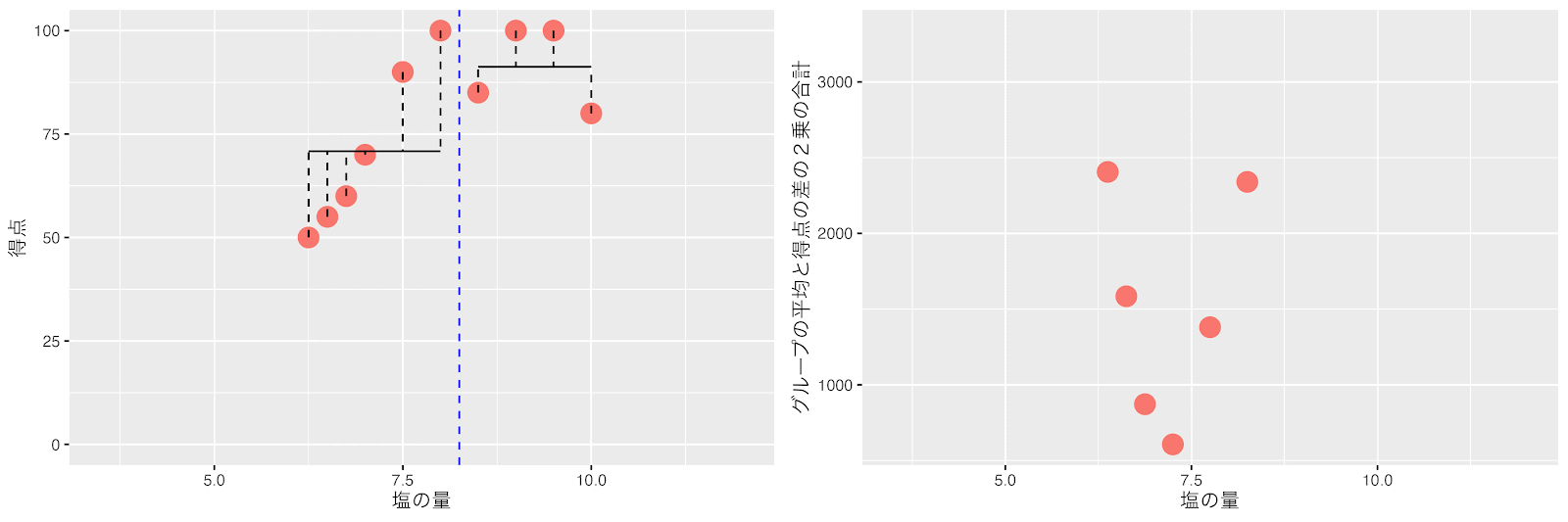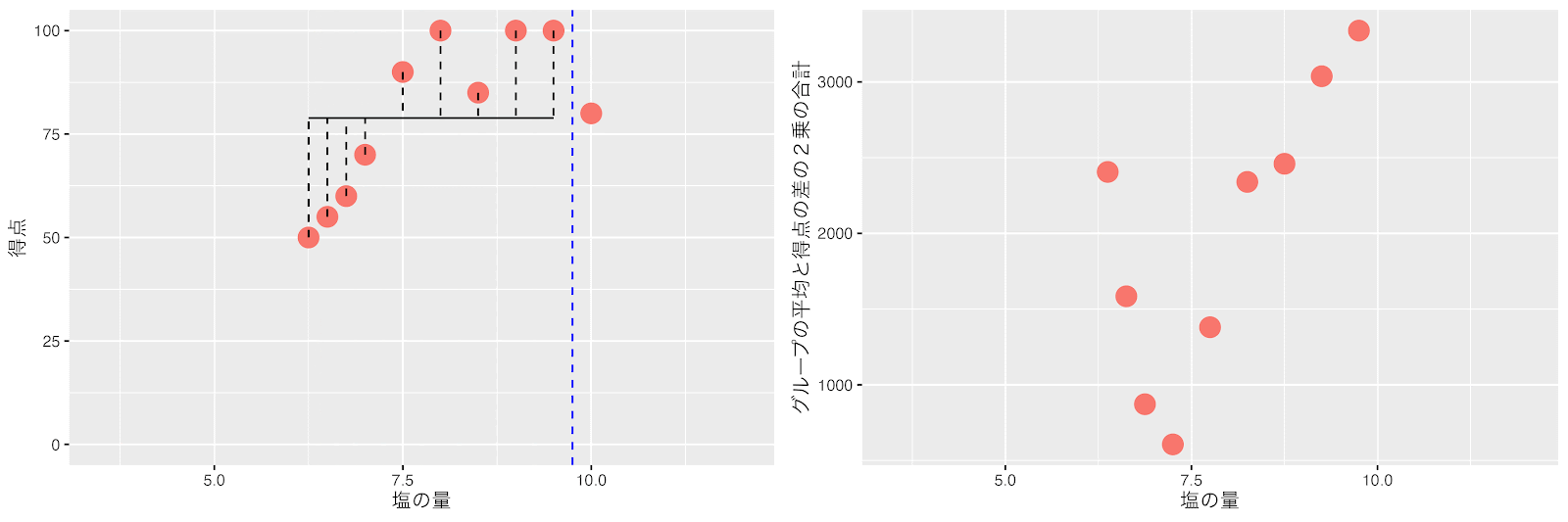
塩の量が7と7.5の間(7.25)のポイントで右と左のグループの平均得点と得点の差の2乗の合計(バラツキ)が最小になるので7.25で分割します。ここで全てのグループのデータ数が7以下になり分割が終了します。
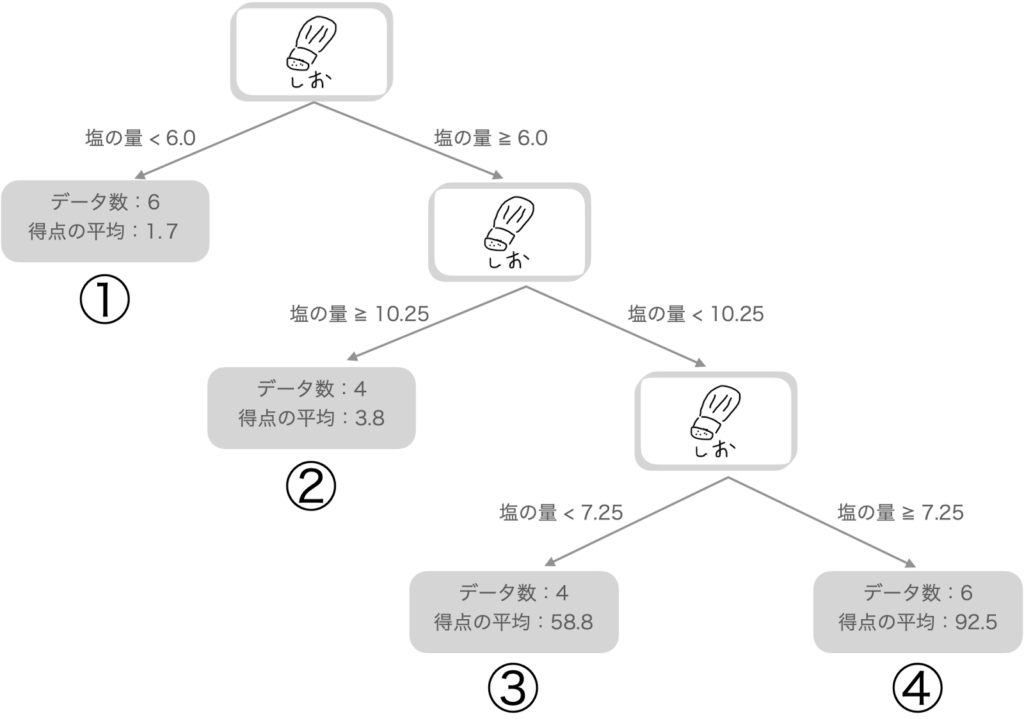
回帰木で学習した結果を最初のグラフに重ねてみましょう。
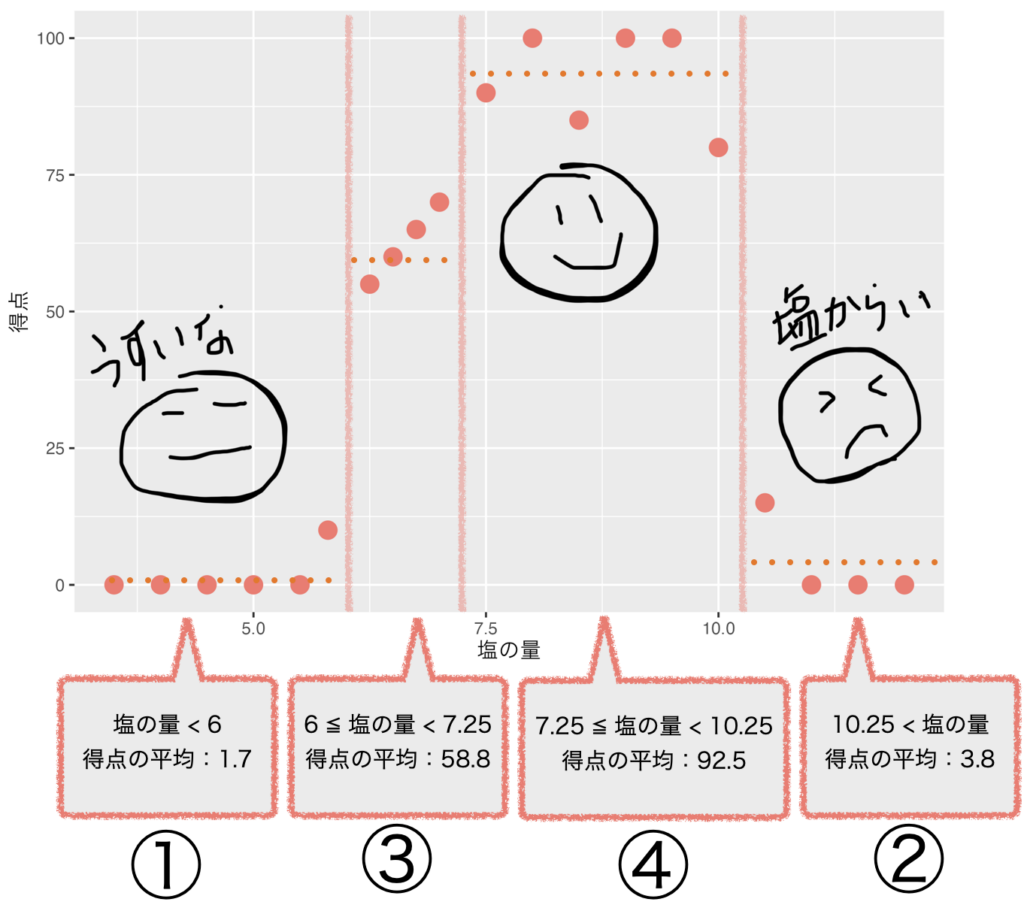
回帰木が分割を何回も繰り返すことで、グラフを見てだいたいこの辺で分ければ良いかなと思ったところで分割されているのではないでしょうか?
この学習結果で、塩の量が7.25から10.25であれば、お料理の得点はそのデータ範囲のお料理の得点の平均である92.5ぐらいになるのかなといったことがわかります。
回帰木が「お料理の得点」に対する、一つのデータ「塩味の濃さ(塩の量)」を学習する仕組みが分かったのではないでしょうか?
それでは、「お料理の得点」に対する、複数のデータの組合せ「塩味の濃さ(塩の量)」「出汁の種類」「出汁の量」を学習する仕組みを見ていきましょう。 「お料理の得点」に対するそれぞれのデータの関係は以下です。
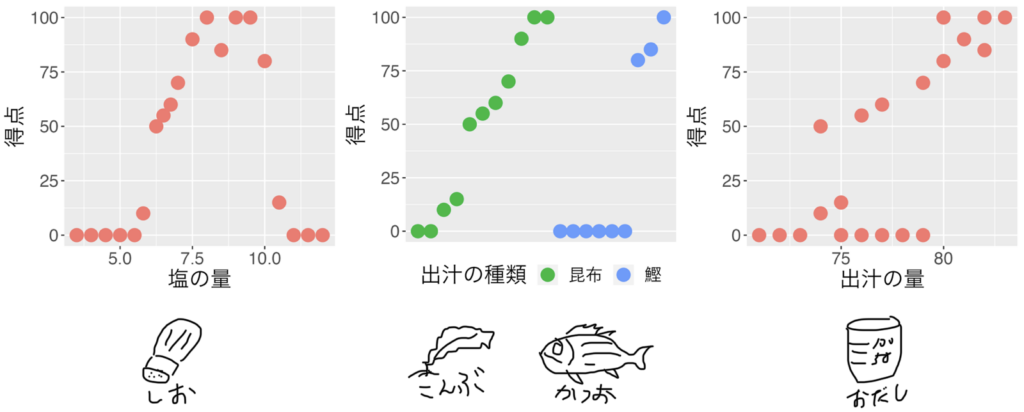
出汁の種類(*真ん中のグラフ)は「昆布」か「鰹」の2つの値しかないですね、このグラフは出汁の種類でプロット点の色を緑と青で表しています。値の小さい順に複数箇所で左右に分けて最小値を探すのではなく「左のグループは昆布」、「右のグループは鰹」とデータを分けるポイントは1箇所のみです。
全てのデータ20個を使って「お料理の得点」に対する、3種類のデータ(塩の量、出汁の種類、出汁の量)を先ほどのように値の小さい順に1個ずつ左と右のグループに分けていき、左と右のグループの平均得点と得点の差の2乗の合計(バラツキ)が最小になる値を計算します。
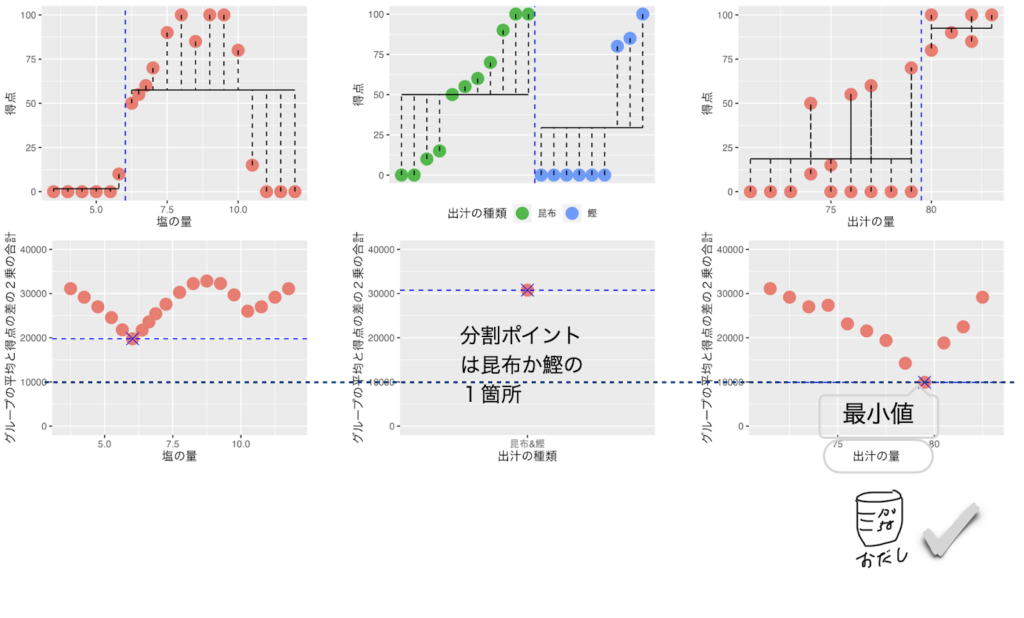
3種類のデータ(塩の量、出汁の種類、出汁の量)で左右のグループの平均得点と得点の差の2乗の合計(バラツキ)が最小になるのは「出汁の量」だということが分かりました。
回帰木は「出汁の量」が「得点」に最も効いているデータと判断します。
この時の出汁の量の左右を分けるポイントは79と80の間でした。 回帰木は、一番最初の分岐として出汁の量が79と80の間の79.5をしきい値にしてデータを分割します。
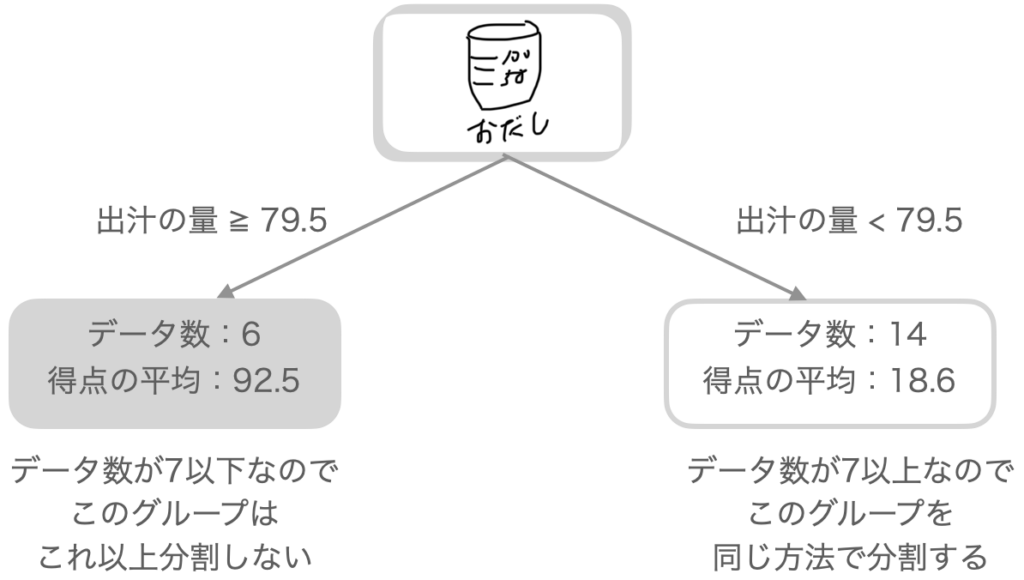
左のグループ(出汁の量が79.5以上)のデータは7個以下の6個ですのでこれ以上分割しません。 右のグループ(出汁の量が79.5以下)のデータ14個を再度、左右に分けて左と右のグループの平均と得点の差の2乗の合計(バラツキ)が最小になる値を計算します。
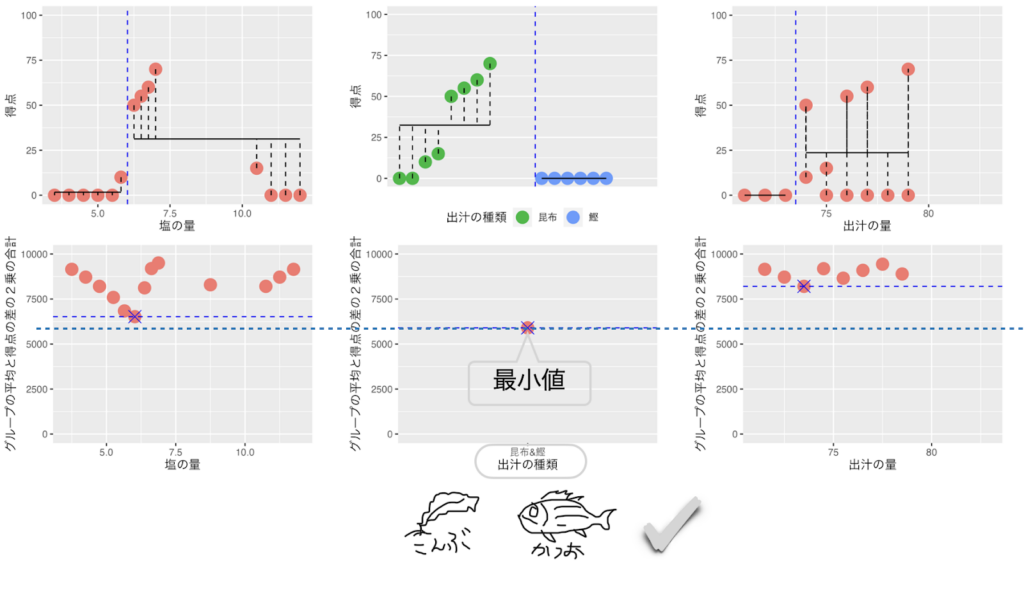
グループの平均と得点の差の2乗の合計(バラツキ)が最小になる値が出汁の種類だということが分かりました。出汁の種類が「鰹」のデータはすべて0点でした。
回帰木は、次の分岐として出汁の種類でデータを分割します。
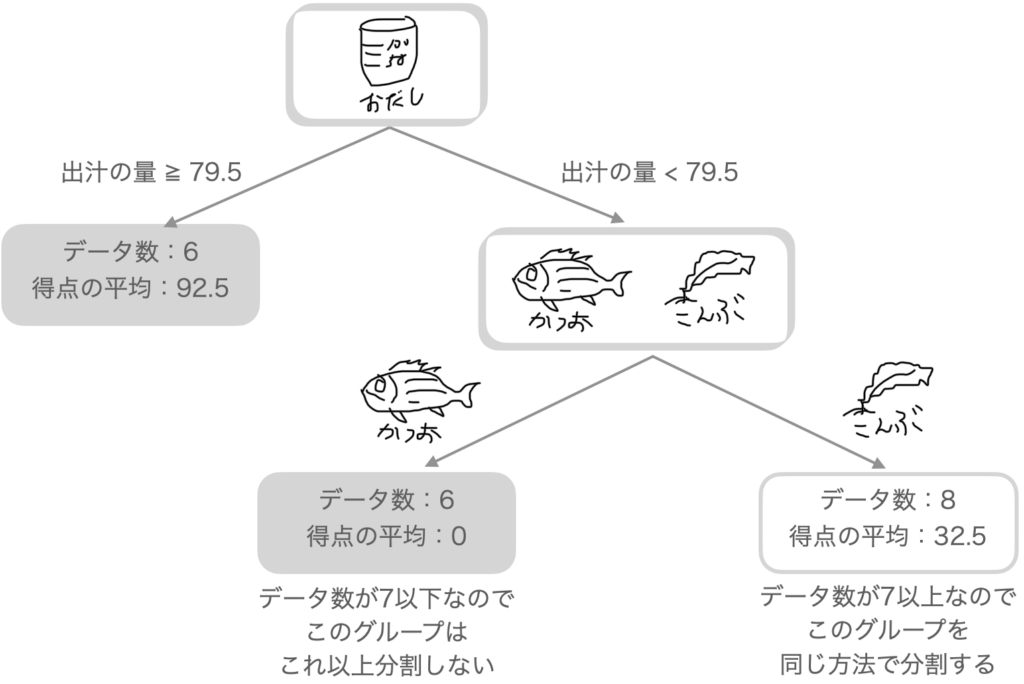
出汁の種類が「昆布」のデータ8個を再度、左右に分けて左と右のグループの平均得点と得点の差の2乗の合計(バラツキ)が最小になる値を計算します。
出汁の種類は「昆布」しかないので昆布の平均値と得点の差の2乗の合計値(バラツキ)を使います。もし、他の項目に比べて、昆布のバラツキが最小になれば他の項目は使われずにここで分割は終了します。(下の図に示すように「出汁の種類」よりも「塩の量」がバラツキが小さかったですね)
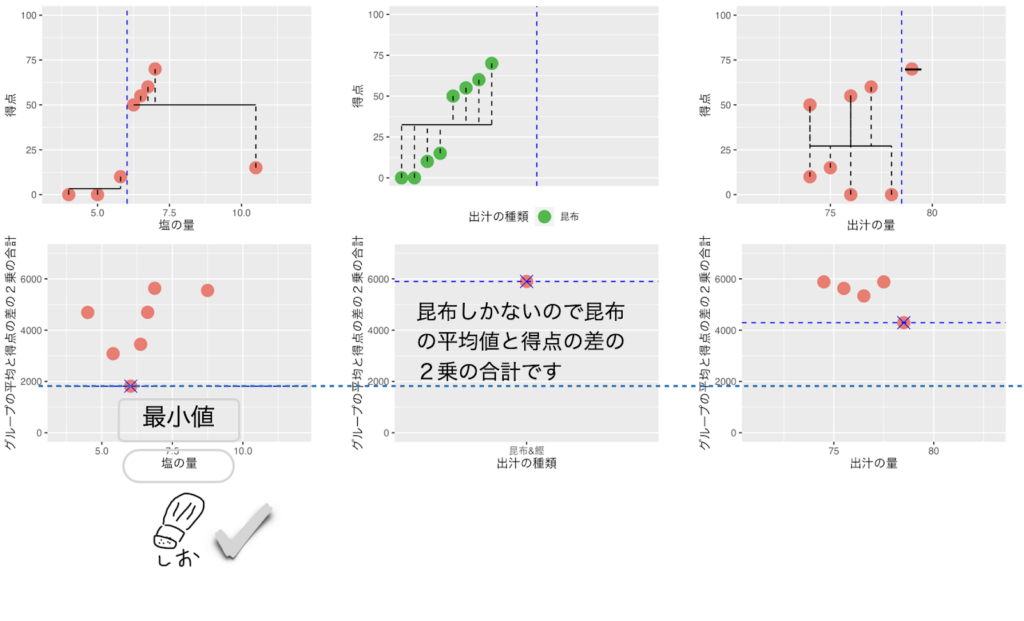
グループの平均と得点の差の2乗の合計(バラツキ)が最小になる値は塩の量で5.8と6.2の中間の6.0を次の分岐として分割したところで全てのグループのデータ数が7以下になり分割が終了します。
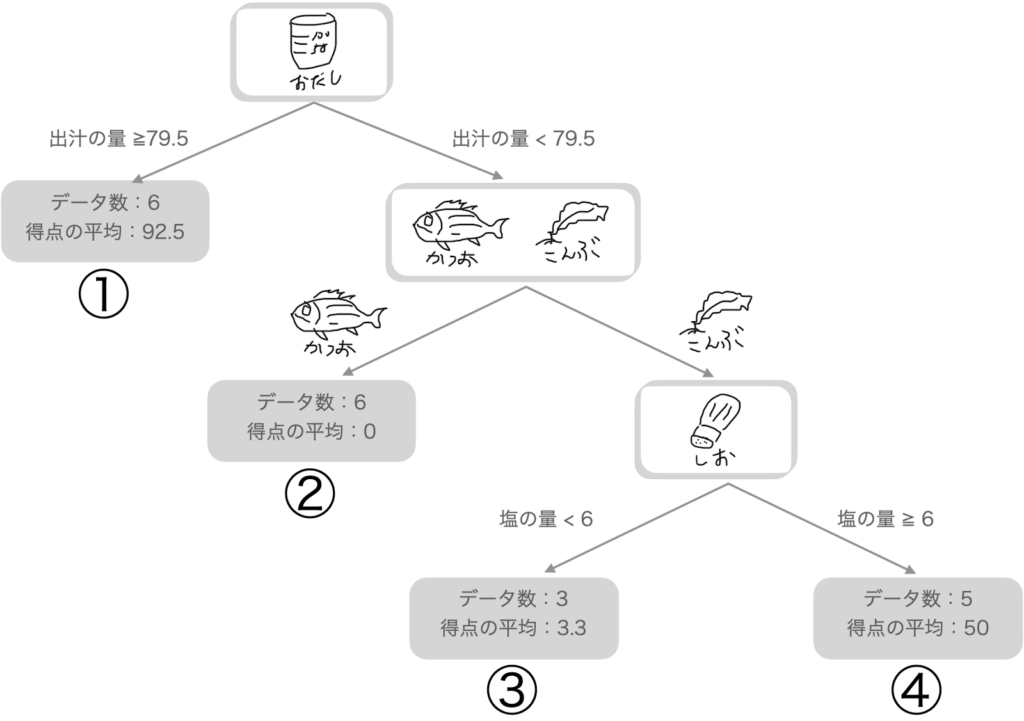
回帰木の学習によって複数のデータの条件でデータを分割する時のルールが自動的に決められたと思います。
機械学習(回帰木)で算出されたルールを使用すれば、①【「出汁の量が79.5以上」】であれば得点が92.5点ぐらいになるのかなとか、④【「出汁の量が79.5以下」&「昆布出汁」&「塩の量が6以上」】の場合、得点が50点くらいといった予測ができるようになります。
お料理の得点に対応するデータ(例:「みりんの量」「お酒 … )が増えてもこの方法で対応することが出来ます。
冒頭の
「機械(コンピューター)がどうやって学習してるの?」への回答として
「機械(コンピューター)がデータのパターンを学習(記憶)する」ために「データのパターンを自動で数式やルールにして記憶する」ことができたと思います。
ありがとうございました。
関連記事



