
友人からの「そもそも機械学習ってなんなの?」「機械(コンピューター)がどうやって学習しているの?」という問いかけをきっかけに機械学習がどのようにデータを学習しているかについてコラムにしてみました。取り上げた機械学習手法は勾配降下法という手法になります。
INDEX
勾配降下法
データ分析を生業にしているものとして恥ずかしいのですが、友人からのある素朴な質問にすぐに答えられなかったことがありました。それは「そもそも機械学習ってなんなの?」「機械(コンピューター)がどうやって学習しているの?」という問いかけでした。
私が考える「機械(コンピューター)がどうやって学習しているの?」への回答は「機械(コンピューター)がデータのパターンを記憶する」ために「データのパターンを自動で数式やルールにして記憶する」だと思っています。
例えば、お部屋探しのサイトで物件をイロイロ見ていると、間取りや床面積や駅までの時間から家賃はこれくらいかな?とか、家賃がこれくらいだと床面積はこれくらいかな?など私たちはデータを無意識に学んで記憶していますよね。
さて、私たちがデータから学んでいることを機械学習ではどのように学んでいるのでしょうか?
「家賃は床面積が大きいほど高い」だろうし、同じ条件であれば「築年数が古いほど安い」など私たちが無意識に学んでいる関係を数式に当てはめてみましょう。
「家賃」=「秘密の数字A」x「床面積」
+「秘密の数字B」x「駅までの時間」
+「秘密の数字C」x「築年数」
+「秘密の数字…」x「…」
+「秘密の数字X」
例えば、無意識に学んでいる「秘密の数字」たちが以下だとします。
床面積が1㎡ごとに家賃がだいたい2000円(秘密の数字A)高くなる
駅までの時間が1分増えるごとに家賃がだいたい1000円(秘密の数字B)安くなる
築年数が1年増えるごとに家賃がだいたい1000円(秘密の数字C)安くなる
基本の家賃がだいたい10000円(秘密の数字X)
お部屋のデータが以下だったとすると「秘密の数字」を使った数式で家賃が想像できます
床面積 = 40㎡
駅までの時間 =15分
築年数 = 3年
家賃 = 「2000(秘密の数字A) x 40(床面積) = 80,000」
+「-1000(秘密の数字B) x 15(駅までの時間) = -15,000」
+「-1000(秘密の数字C) x 3(築年数) = -3,000」
+「10000(秘密の数字X)= 10,000」
家賃 = 80,000 +(-15,000)+(-3,000)+10,000 = 72,000
このような具合に、私たちはお部屋探しサイトで物件情報を見ているうちに、無意識に「秘密の数字」たちを学習して家賃を想像できるようになったりします。
機械学習も同じように、家賃とそれに紐づくお部屋のデータから左側の「家賃」と右側の計算式で算出された値の差が一番小さくなるように「秘密の数字A, B, C, … , X」を自動で決めて数式を完成してくれます。
機械学習で、この「秘密の数字」たちを決める仕組みの一つに勾配降下法というものがあります。
水は何もしなくても高いところから低いところに流れていきますよね。
勾配降下法も同じで、高いところ(大きい値)から低いところ(小さい値)を探していって一番低いところ(小さい値)で自動的に止まる仕組みです。
それでは、私が考える機械学習のキモ、自動で数式を完成してくれる仕組みの勾配降下法をみていきましょう。
分かりやすくするために、お部屋のデータの「家賃」と「床面積」だけを使います
「家賃」=「秘密の数字A」x「床面積」
+「秘密の数字B」x「駅までの時間」
+「秘密の数字C」x「築年数」
+「秘密の数字…」x「…」
+「秘密の数字X」
「家賃」=「秘密の数字A(傾き)」x「床面積」+「秘密の数字X(切片)」
「秘密の数字A」は傾きと呼ばれ、床面積が1増えたときの家賃の増加分です。
「秘密の数字X」は切片と呼ばれ、床面積が0の時の家賃になります。
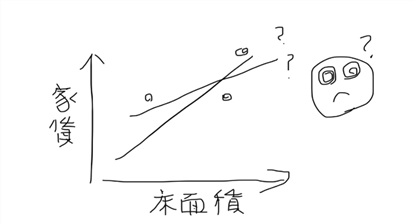
秘密の数字の組合せは無数にあって組合せによって無数に線が引けてしまいます。
勾配降下法がこの「秘密の数字A」(以後:傾き)、「秘密の数字X」(以後:切片)を最適化する仕組みをみていきましょう。
最初に「傾き」を固定して「切片」を最適化する仕組みを理解します。
この仕組みが理解できたところで「切片」と「傾き」を同時に最適化して式を完成したいと思います。
まずは、傾きを1に固定して切片の値を最適化してみます
「家賃」=1x「床面積」+「切片」
切片にはテキトウな数字、0を使ってみましょう。
実際の家賃と比べるとかなり下のほうに直線が引かれました。
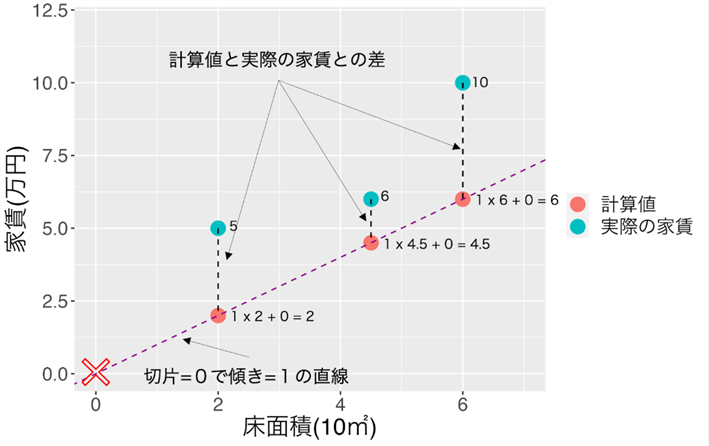
今回は「計算値と実際の値の差の2乗の合計」を使って計算で引かれる点線を実際の値に最適化していきます。「計算値と実際の値の差」を以降、残差と呼ぶことにして「残差の2乗の合計」*とします。
*「残差の2乗の合計」は機械学習用語の損失関数の一つです。(損失関数はイロイロあって用途によって使い分けますがそれはまたの機会に)
それでは損失関数「残差の2乗の合計」を計算していきます。
傾きが1で切片が0の時の床面積2の計算値は2×1+0 = 2万円になります、実際の家賃が5万円ですので、残差の2乗は、(2-5) = -3、-3の2乗 = 9と計算できます。
この調子で床面積4.5の時と床面積6の時の残差の2乗を合計すると27.25という値が得られます。

傾きは1に固定して、テキトウに決めた切片を0から0.5ずつ増やした時の損失関数の「残差の2乗の合計」の値の変化を見てみましょう。
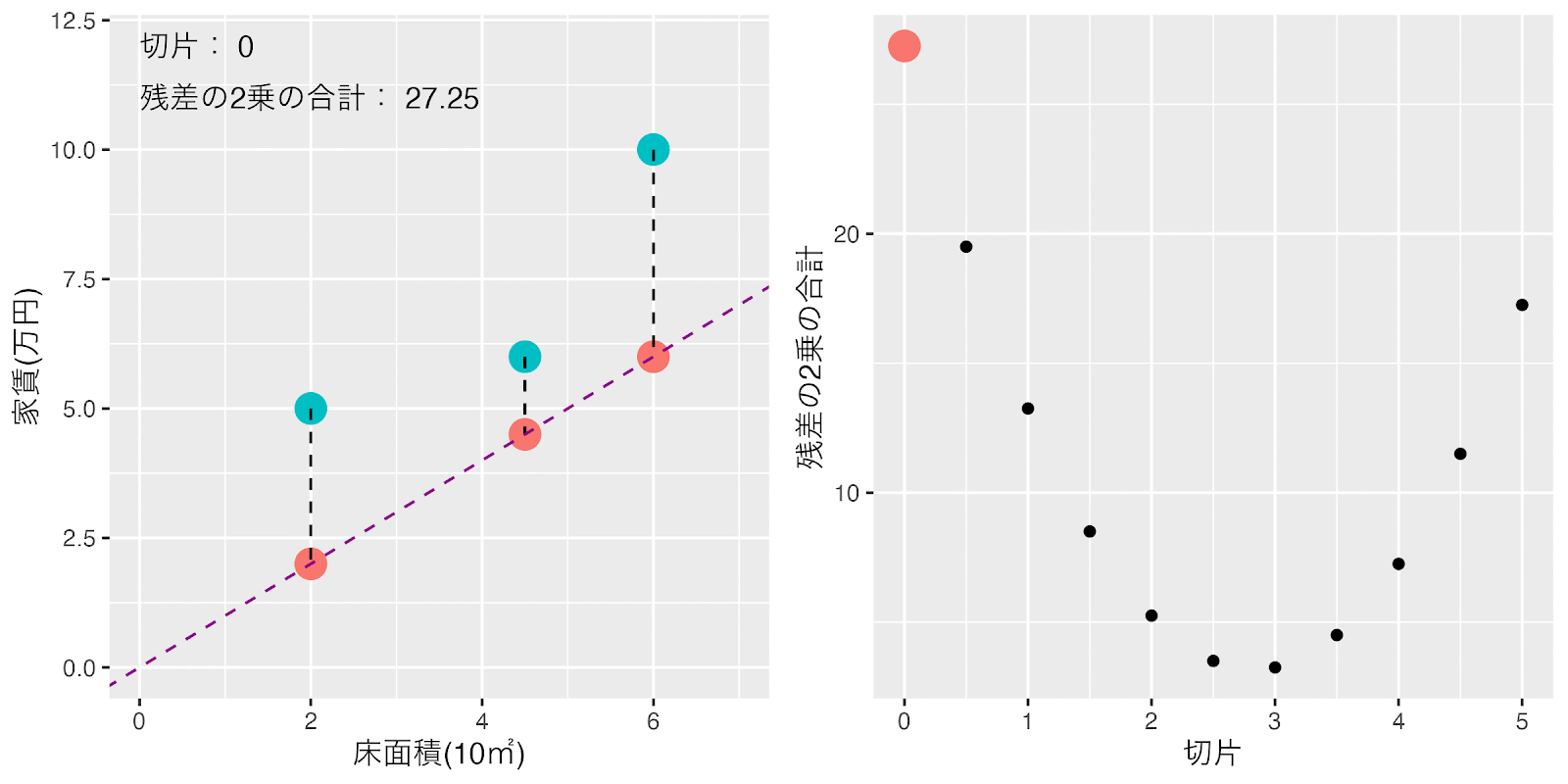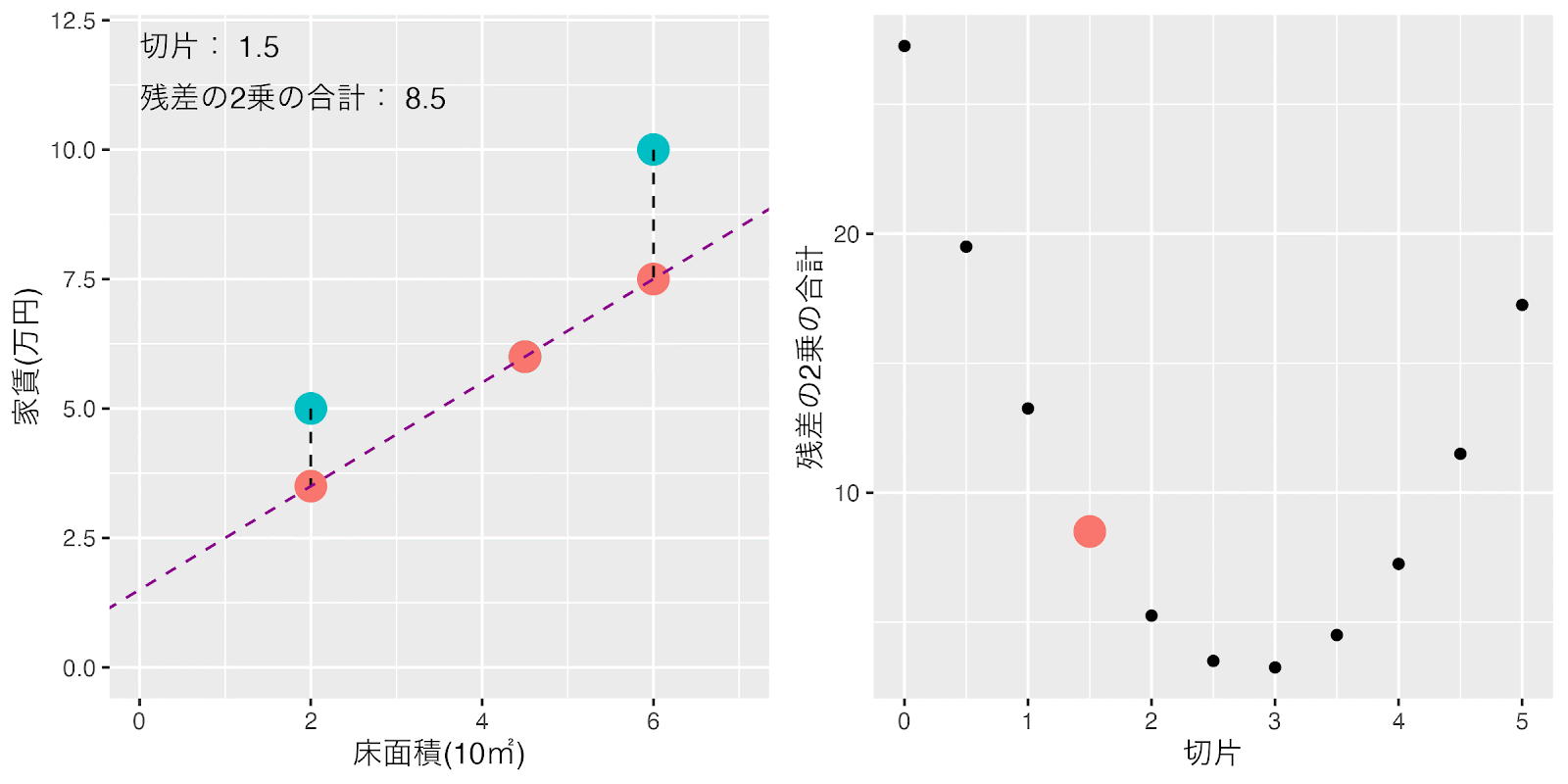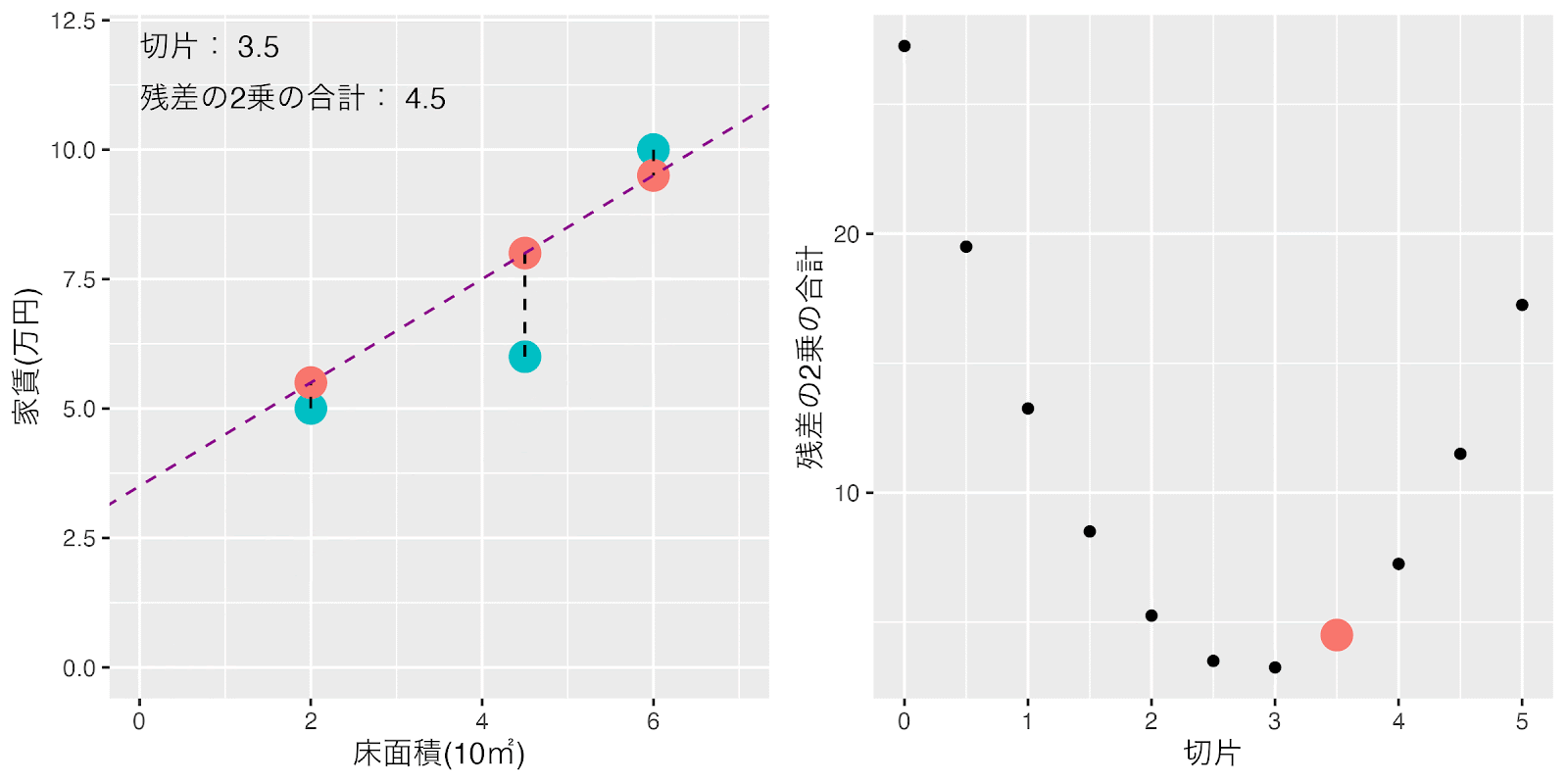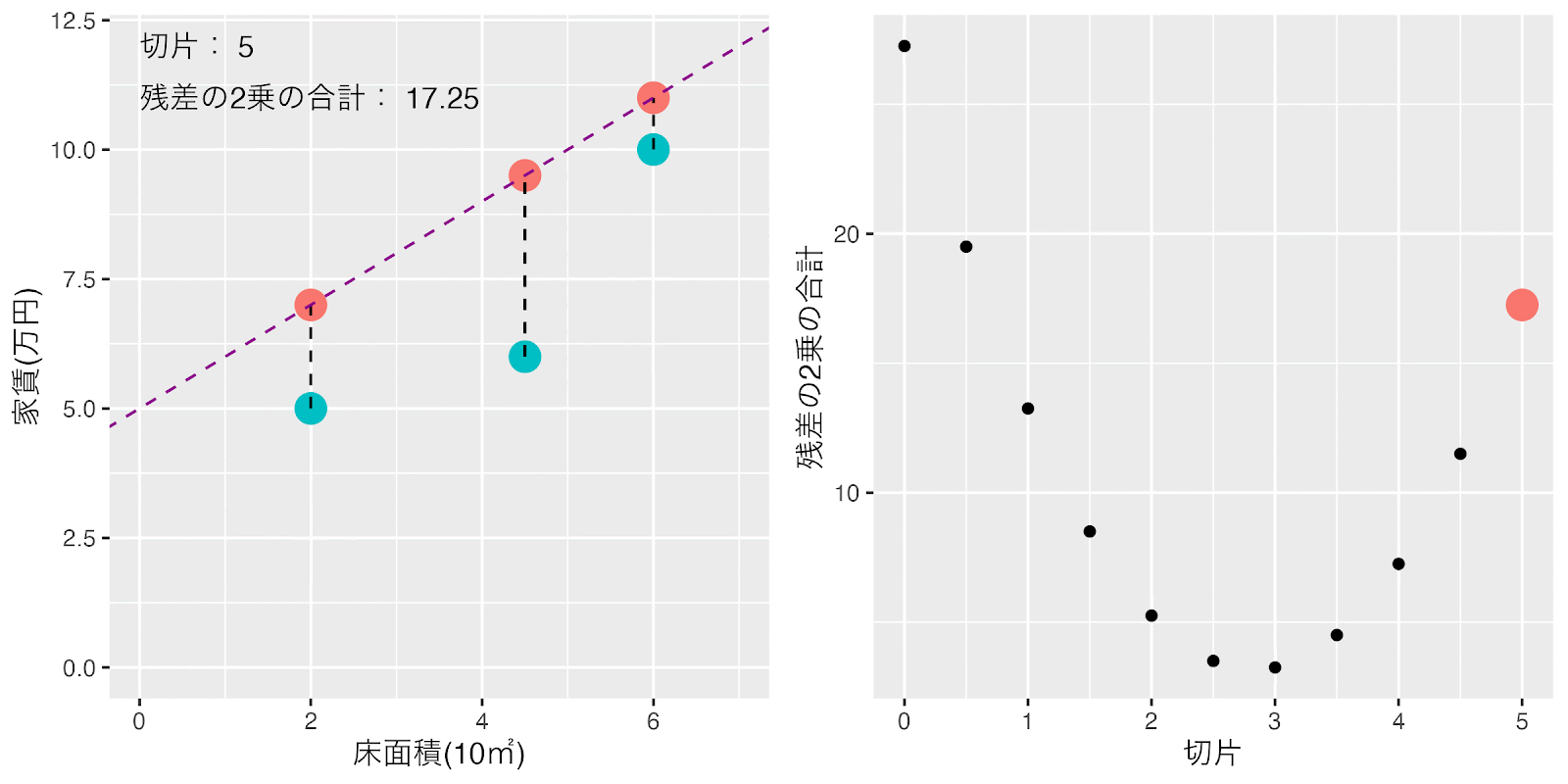
切片を増加させていくと切片が3の近辺で「残差の2乗の合計」の値が最小に近づきそうだということが分かりますね。
次に、この「残差の2乗の合計」の値が最小になるポイントを探すときの仕組みをみていきましょう。
上のアニメーションの右側のグラフで示される切片を変化させた時に引かれる曲線の接線の傾きが0になるポイントを探せばそこが「残差の2乗の合計」の値が最小になるポイントになります。
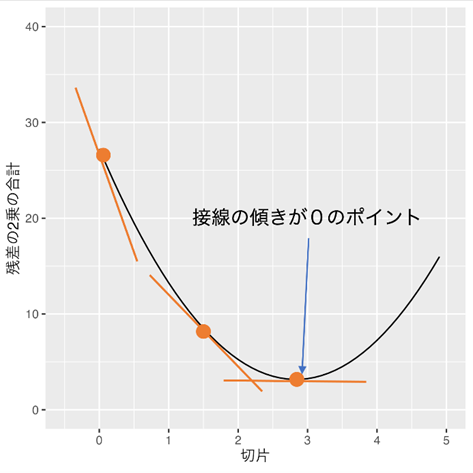
切片の各ポイントの「残差の2乗の合計」接線の傾きは「残差の2乗」の切片の偏微分値の合計で求めることができます。
まずは「残差の2乗」の計算式を切片で偏微分する時の偏微分式変形ルール*で変形します。
偏微分式変形ルール*:偏微分で検索するとルールの解説があります、本コラムでは割愛します。
1.カッコ内の式(残差の計算式)のべき乗(2乗なので2)を式の前に持ってきます。

2. 切片には係数がない、つまり切片の1倍なので、先に移動させた2を1倍します

切片の偏微分式が出来ました。傾き=1と切片=0の時の「残差の2乗の合計」の接線の傾きを求めてみましょう。

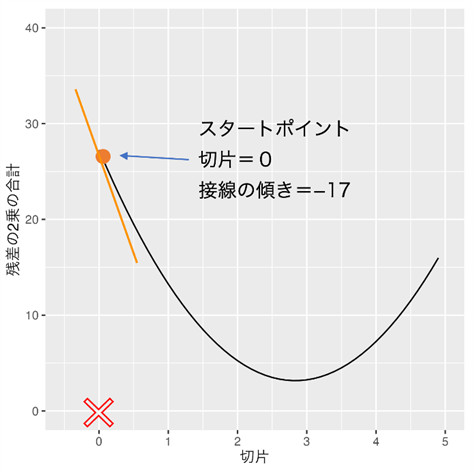
スタートポイント(切片=0)の接線の傾きが−17と求まりました。
次に切片を移動させていって接線の傾きが0に最も近くなるところを探していくのですが、この時に使うのがラーニングレートという値です。
仮にラーニングレートを0.1(*巻末注1)にして、どちらの方向に、どれくらい移動させるかの「ステップ値」を決めてみましょう。
「接線の傾き」 x 「ラーニングレート」 = 「ステップ値」
-17 x 0.1 = -1.7
初めの「切片=0」から、「ステップ値=(-1.7)」を引くことで次に計算する「切片」が決まります。
0 – (-1.7) = 1.7
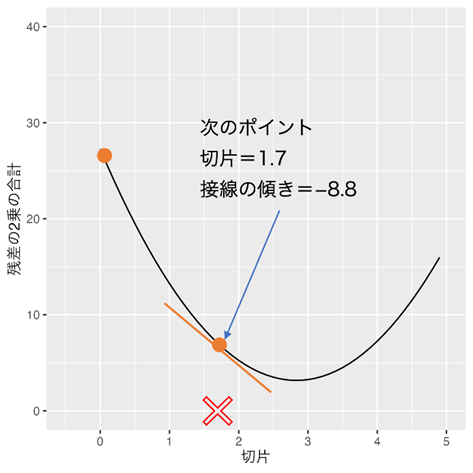
正しい方向(接線の傾きが降っている方向)に移動しましたね(✔️1*)。
(✔️1*)接線の傾きがマイナスのときは右に、接線の傾きがプラスのときは左に移動します。
同じように切片=1.7の時の接線の傾きを求めます。

切片=1.7の時の接線の傾きは-8.8と求まります。
再度ラーニングレート0.1をかけるとステップ値は-0.88になります。このステップ値を、接線の傾きを求めた切片1.7から引くと次に計算する切片の値が求まります。
1.7 – (-8.8 x 0.1) = 2.58
このように計算を続けると以下のように、接線の傾きが小さくなるにつれてステップ値が小さくなっていきます。最後に接線の傾きが十分に0に近くなる閾値(例:0.001)以下になった時に計算を止めます。
その時の切片の値が「残差の2乗の合計」の値が最小になるポイントとして算出されます。
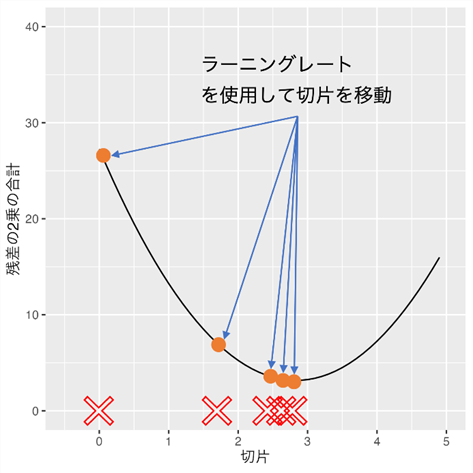
ここまでは、傾きを1に固定して切片を最適化したのですが、勾配降下法は、ふたつ以上の値の組合せを同時に変化させて損失関数(「残差の2乗の合計」)の値が最小になるポイントを探すことができます。
「切片」の偏微分の式は先ほど作成しましたので、今度は「傾き」の偏微分の式に変形してみましょう。
1.カッコ内の式(残差の計算式)のべき乗(2乗なので2)を式の前に持ってきます。

2. 傾きは「床面積」倍されているので、先に移動させた2を「床面積」倍します。

切片と傾きの偏微分の式ができましたので「切片」を0「傾き」を0からスタートさせて、ラーニングレート0.001(*巻末注1)で「切片」と「傾き」の値を同時に移動させてみましょう。

このように計算させていくと「切片」と「傾き」それぞれの「偏微分値の合計(接線の傾き)」が自動的に0に近づいていきます。接線の傾きが十分小さくなったところで止めれば「損失関数(「残差の2乗の合計」)」が最小になる「切片」と「傾き」の値が求まります。
「切片」を0「傾き」を0からスタートさせて「損失関数(「残差の2乗の合計」)」が最小になるまでの「切片」と「傾き」それぞれの「偏微分値の合計(接線の傾き)」の変化の様子をアニメーションでみてみましょう。
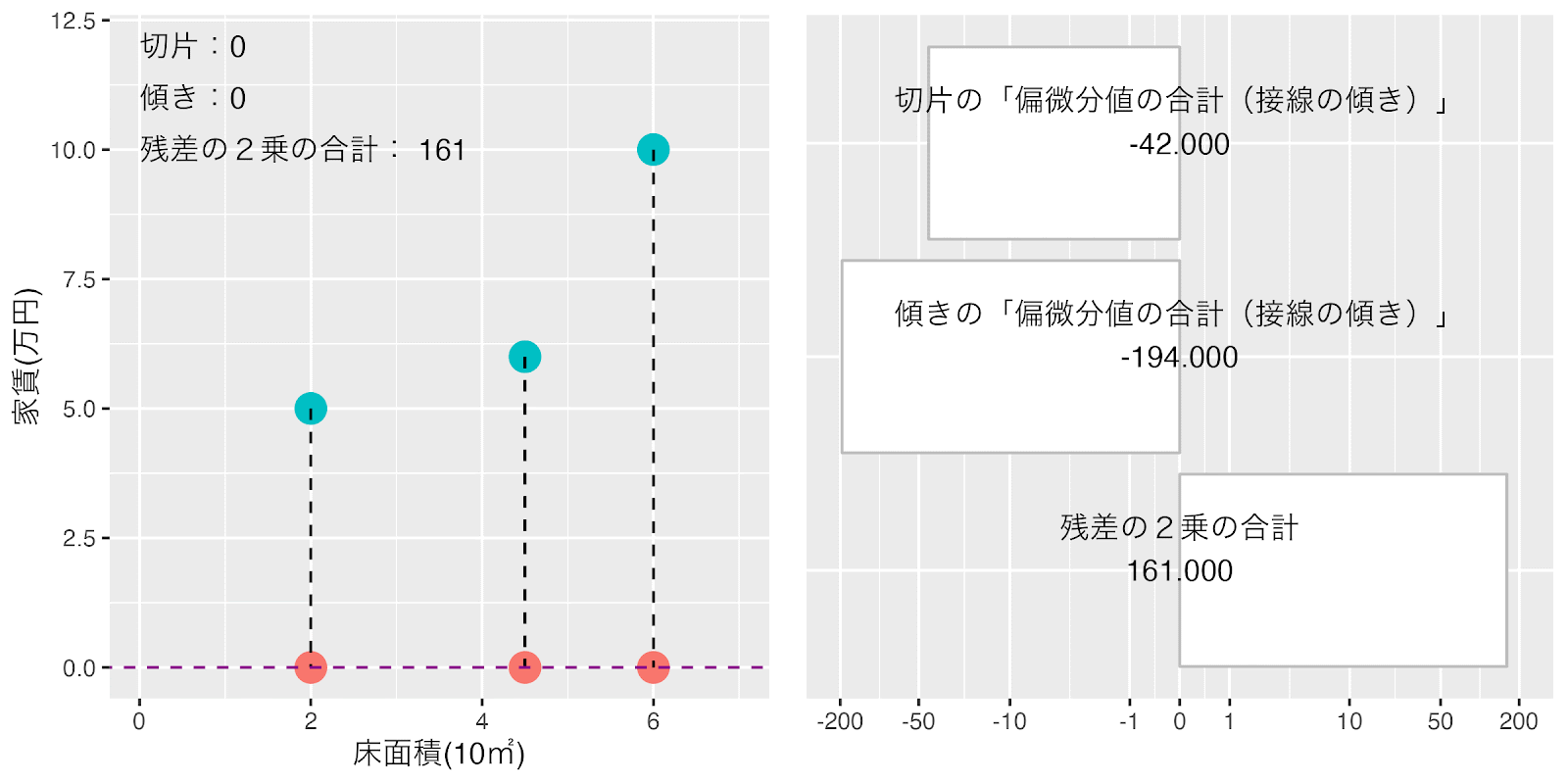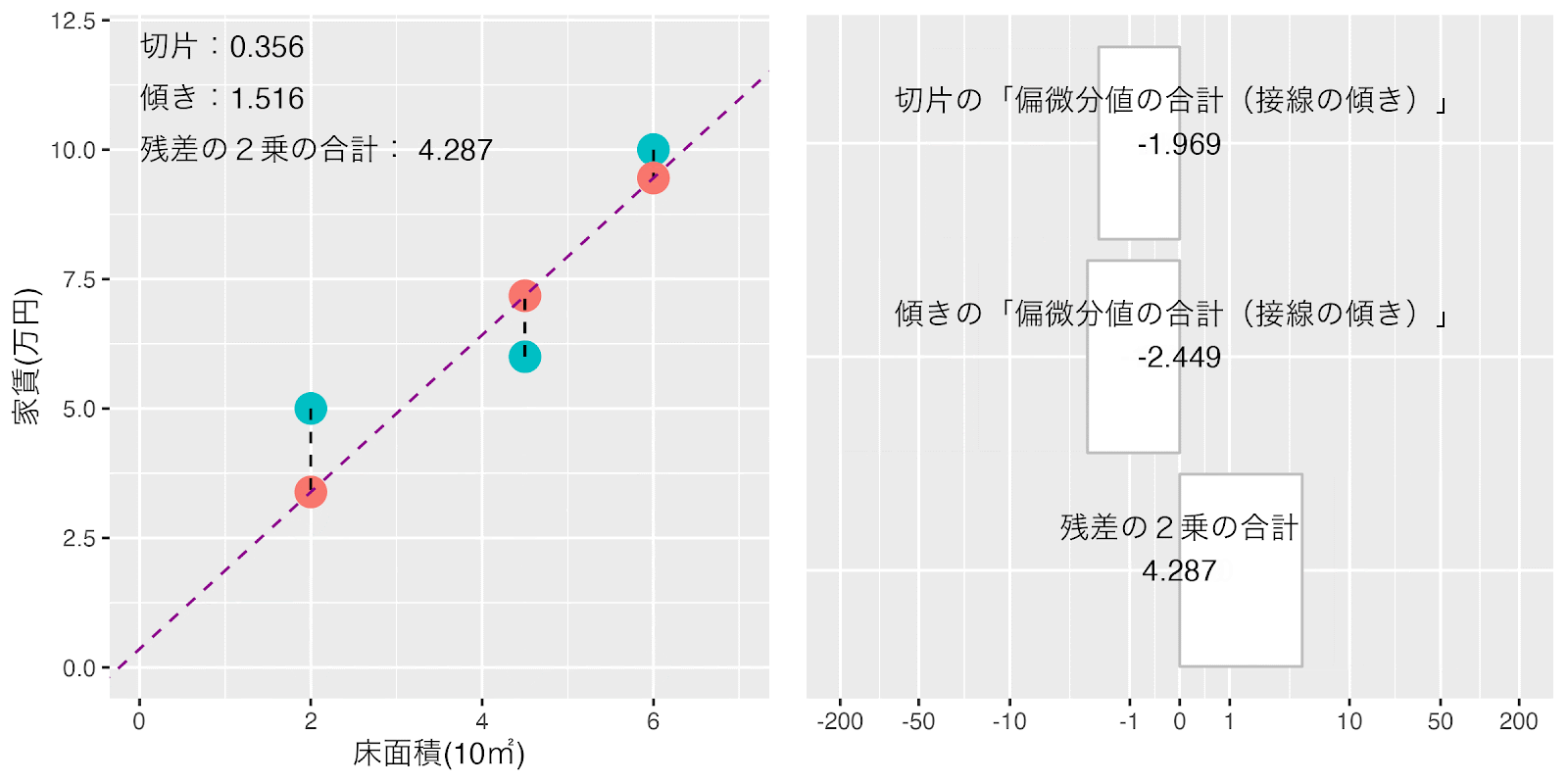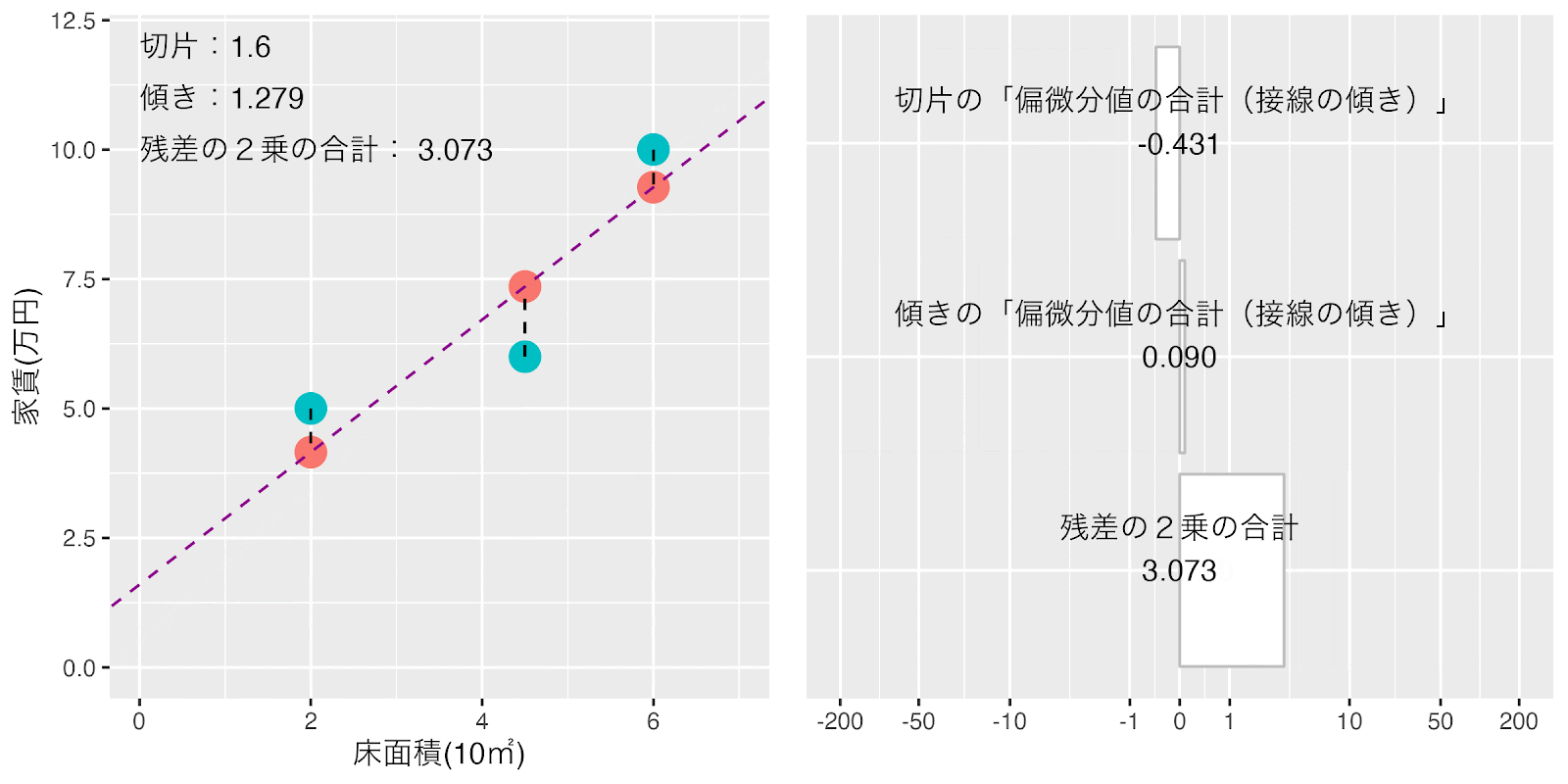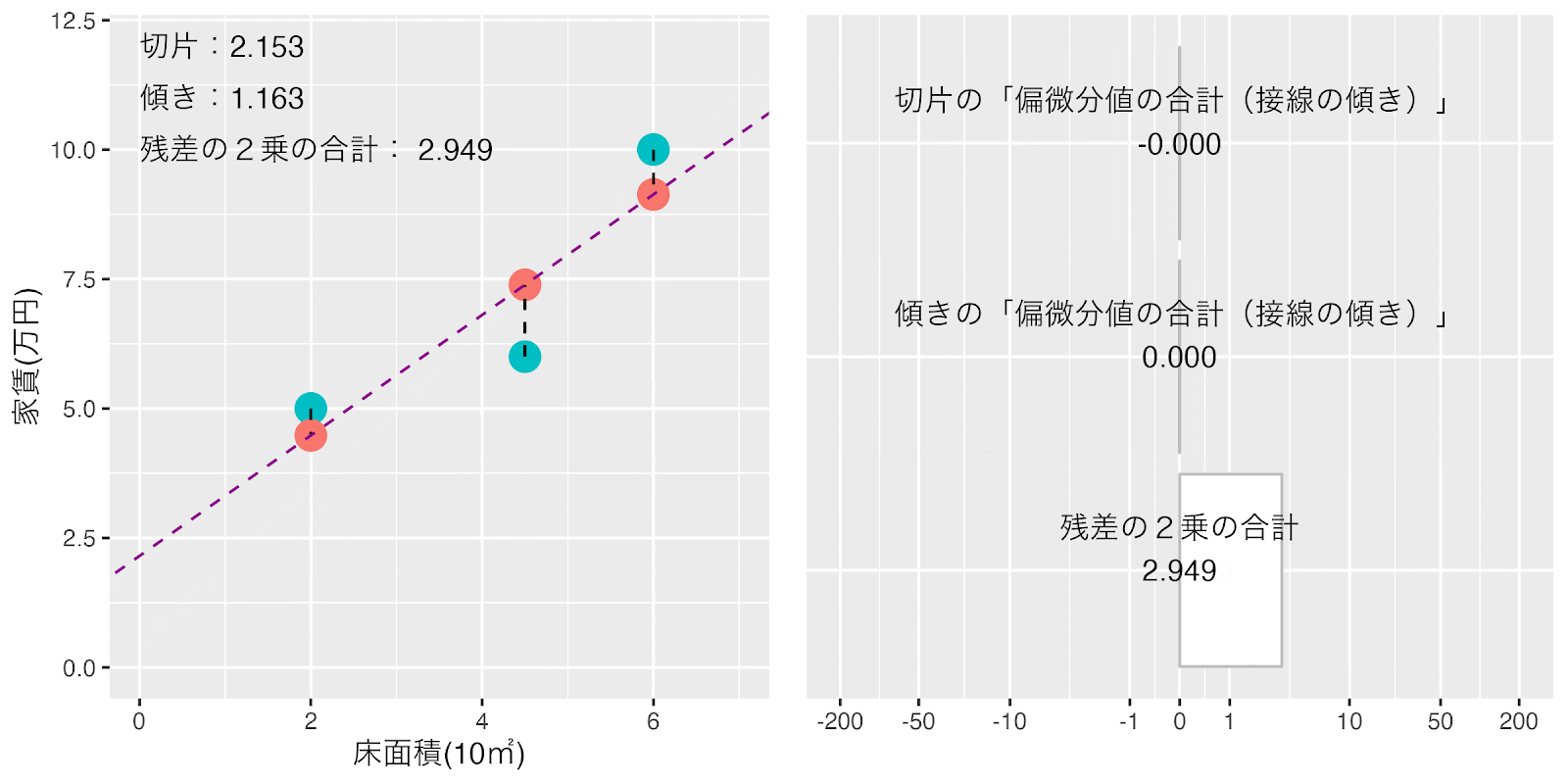
「損失関数(「残差の2乗の合計」)」が最小になる「切片」と「傾き」が自動的に求まり、家賃を説明する式が完成しました。
「切片」= 2.153
「傾き」= 1.163
「家賃」=1.163 x「床面積」+ 2.153
勾配降下法は「駅までの時間」や「築年数」など家賃に付随する他のデータ項目を追加すれば「損失関数*」が最小になるように、それぞれのデータ項目(「駅までの時間」、「築年数」…)に対応する「秘密の数字」を算出して数式を完成してくれます。
*損失関数として今回は「残差の2乗の合計」を使用しましたが、勾配降下法は他の損失関数でも同じ仕組みで使用できます。
冒頭の
「機械(コンピューター)がどうやって学習しているの?」への回答として
「機械(コンピューター)がデータのパターンを記憶する」ために「データのパターンを自動で数式やルールにして記憶する」ことができたと思います。
ありがとうございました。
今回は機械学習の基礎となる知識をできるだけ簡単に説明してみました。
使い方次第は便利なツールであるというイメージが少しは持てましたでしょうか?
もし機械学習を使ったら「こんなこともできちゃうのかな?」みたいなご質問があれば
遠慮なく、お問い合わせフォームにご連絡いただければと思います。
またこのような仕事に興味がある方も積極採用しておりますので、応募お待ちしております。
巻末注1*
ラーニングレート
勾配降下法におけるラーニングレートの決め方
最初に0.001を使用して計算し、順次値を大きくしていき(0.001 → 0.003 → 0.01 → 0.03 → 0.1)損失関数の減少の仕方を比較する方法が多く使われています。
ラーニングレートは大きくなるにつれて計算量が少なくなるというメリットがありますが、ある閾値を超えて大きくすると損失関数の値が減少しなくなります。
AI・データ分析サービス
https://www.tis.jp/service_solution/data-analytics/
データ分析・AI人材育成支援サービス
https://www.tis.jp/service_solution/ai-education/
関連記事



